-0.15 Phase
-0.1 Topology of time
-0.05 Stitching time
0 Emergent properties
0.05 Direction selectivity
0.1 Adaptation and direction selectivity
0.15 Learning direction
0.2 Receptive fields as sheaves
0.25 Globalization
0.3 Behavior
0.35 Physics and Philosophy
0.4 The direction of time
0.45 Music
0.5 Film
0.55 Arguing
0.6 Appendix
0.7 Afterword
A fascinating group of people living in Amazonia, the Piraha,
typically do not regard the past and future as meaningful.
As anthropologist/linguist Daniel Everett describes them, unless they experienced something for themselves,
or were told about something by somebody else who they know, it doesn't exist.
That probably seems foreign to most readers. We are commonly taught about history,
with a desire to go way back, and even learn about many things that are not likely to be relevant to us, ever.
We frequently consider and imagine future expectations.
Time travel fascinates many people, unlikely though it might be. Our view of time reflects these obsessions.
But to what extent are these acquired and conditioned? Take a few minutes to think about how you view time.
What picture would you draw to illustrate time?
Most of us were probably taught in early childhood that time should be thought of as a line,
projecting back to the past toward the left and projecting forward to the future toward the right.
This model of time dominates thinking in Western science.
Time is considered to be one-dimensional, and totally ordered.
That means that a relation between points in time exists where we can say that for any two points,
one comes before the other (Fig. 1). That sounds natural to most people, but is subject to question.
The best-known such question is which came first, the chicken or the egg? Similarly, which comes first, noon or midnight?
Such counterexamples illustrate that there might be a problem with this conventional notion of time as totally ordered points on a line.
The problem is that points in time do not correspond to when things occur.1
Conventional views of time
Timeline, moments, simultaneity, reality of time, alternative views


Despite this idea that time is a sort of track that we ride on in a single direction, we can't directly observe where we are on that rail.
Einstein showed that this view of time as points on a line doesn't make physical sense.
He detailed how, in order to measure two events as having happened at the same time,
observations of the events are needed, and these observations take time because of the finite speed of light
(the highest speed that can be reached, see Physics and Philosophy below).
If two stars at opposite ends of our galaxy went to supernova,
they might appear to explode simultaneously to your friend Stella equidistant from them,
even though they will appear to occur at different times to you out at a point nearer to one of the stars (Movie 1).
Which came first, α or β? So time depends on space (and other factors).
We are accustomed to the lack of simultaneity of our clocks located at different places on the earth.
We have conventionally designated 24 (plus some odd ones) time zones,
with the clock time increasing by one hour
(with exceptions like Newfoundland)
when crossing into a new zone from west to east.
We even deal with the fact that this arrangement increments the date at the International Date Line
when going east to west.
The reason for this lack of apparent simultaneity across the globe is that we like to have clock times
correspond with the rotation of the earth. This makes sunrise and breakfast occur around 6 am, high noon and lunch around 12,
and sunset and dinner around 6 pm. People in different time zones do not eat their meals simultaneously.
Note that those correspondences of sunrise and sunset are only true at a set of disjoint points
on the equator and on the vernal and autumnal equinoxes. More importantly, the correspondence varies with latitude.
The clock times of sunrise and sunset vary with the seasons.
Even the seasons are reversed between the north and south over the period of a year.
And more tropical regions don't have the seasons those of us in the north and south experience: wet and dry seasons are typical.
We are less accustomed to the fact that a clock sitting on a mantel runs faster than an identical clock on the floor.
The difference is quite small, but we have clocks that are precise enough to measure it. As Einstein also showed, time is affected by gravity.
Gravity is actually the same thing as space, so the effect of gravity on time can be seen as warping spacetime.
All of these phenomena become clearer when working in the frequency domain, as discussed throughout this treatise.
In the frequency domain, we rely on frequency and phase. Sometimes period, the reciprocal of frequency, substitutes.
The daily (period of 24 hours) rotation of the earth gives us time zones (phases),
and the annual (period of a year) orbit of the tilted earth around the sun produces seasons (phases).
We understand that spatial phase varies continuously around the lines of latitude,
and temporal phase is equal to that at the period of a day.
Greenwich England's longitude (0°) and New Orleans USA's longitude (90°) are separated by ¼ of the way around the earth,
meaning they are 6 hours apart, ¼ of the day (during standard time).
Gaborone Botswana and Tallinn Estonia are at about the same longitude, but differ in latitude by about 84°,
making them about ¼ cycle apart on a south-north-south great circle.
Sunrise that occurs at 6:48 am in Gaborone occurs at 5:23 am in Tallinn on August 9.
We can easily calculate these astronomic predictions in the frequency domain, based on phases and periods.
Analogous practical and theoretical gains are obtained in neuroscience.
We only know about time because our brains have neurons whose activity changes with time.2
As Einstein recognized that an observer is needed to know about timing,
we need to recognize that our brains need to respond to changes in the world with changes in activity
to know about timing. Like the finite speed of light,
neurons only respond to changes in the world after some finite time, usually thought of as latency.
Our brains don't know when an event occurs, it only has the information from its activity,
and that activity does not change simultaneously with the event.
The time when an event occurs can only be known relative to when another event occurs.
Philosophers have long argued about the reality of time. One of my childhood heroes,
Parmenides3,
considered time to be an illusion: "coming into being is extinguished and perishing is unheard of."
Although this concept is fairly common in philosophy (e.g., St. Augustine,
Avicenna,
Bergson,
and Russell),
most of western science takes time to have some reality.
In physics, time is often combined with space into one structure that is influenced by matter, although interpretations can vary.
Einstein, and many other physicists, agree(d) with Parmenides that time is an illusion (perhaps).
A physical description of the universe has been proposed, the Wheeler-DeWitt equation, in which time does not exist.
Outsider physicist Julian Barbour (The Nature of Time) shows how time is an abstraction.4
He quotes his touchstone Ernst Mach: "It is utterly beyond our power to measure the changes of things by time ...
time is an abstraction at which we arrive by means of the changes of things;
made because we are not restricted to any one definite measure, all being interconnected."
Barbour himself echoes Parmenides: "The [theory] I favour seems initially impossible:
the quantum universe is static. Nothing happens; there is being but no becoming. The flow of time and motion are illusions."
Barbour proposes a lovely metaphor: "Unlike the Emperor dressed in nothing, time is nothing dressed in clothes.
I can only describe the clothes."
When we supposedly measure time, we are using one process that depends on time to measure another process that depends on time.
Galileo supposedly measured his pulse rate by counting how many oscillations a chandelier made.
Rovelli chapter 7 provides an excellent discussion of this, rephrasing Barbour's quote above:
"'Physics without time' is physics where we speak only of the pulse and the chandelier, without mentioning time."
A runner's pace is measured with a stopwatch that counts ticks of some kind produced by the pendulum-like mechanisms inside the watch.
Mach recognized that time doesn't have any yardstick of its own.
Carlo Rovelli ends the first section of his book The Order of Time with these thoughts:
Werner Heisenberg established famed limits on the precision to which time can be measured.
The Planck time (on the order of 10-43 seconds - unimaginably precise, practically speaking;
the Planck length is about 10-33 centimeters) can be considered as the smallest period of time.
Points on the time line are called moments, and receive a lot of attention. Often, the most important moment is thought of as "now", quite an elusive concept (Muller; note his discussion of free will at about 50:40).
Experiences are associated with moments in time. Those experiences have some duration, however,
so we should be leery of moments as single points in time. Whether or not two moments can overlap in time seems unclear.
"There is no nature apart from transition, and there is no transition apart from temporal duration.
This is why an instant of time, conceived as a primary simple fact, is nonsense" (Whitehead 1938, p. 207).
Most neuroscientists might argue that our experiences do occur at moments in time, and can be thought of as events,
with brief durations. These events are associated with activity in neurons, and the time between an event and the neuronal activity,
the latency of the response, is often considered the basis for our sense of time.
To repeat for emphasis, people think this even though the only knowledge we have is when the activity occurred relative to other neural activity -
we don't directly know when the event occurred. Furthermore, our experience is seldom localized in time to the degree expected from that view.
When a very brief experience occurs, in order to be detectible it needs to be strong.
We don't experience weak, subtle things that are only present for a few milliseconds, especially considering that our experiences do not occur in isolation,
but instead over a complicated background that can be considered noise in the context of detecting a particular feature.
Consider that much of our experience consists of feelings, and whether it's even possible to experience an emotion for only milliseconds.
More importantly, most neuroscientists, and most people in general, think of time in terms of conscious processes.
Almost all of what the brain does does not enter our consciousness.
We think about time often enough. For example, when we're late we think about having to go faster.
But when we hear somebody talking, we normally don't think about how the sounds change over time.
When we watch leaves rustling in the wind, or waves at the beach, we don't normally pay attention to the timing of their motion.
When we walk, we don't normally worry about how we're moving our feet. Everything we do, we do over time.
We are unaware of most everything we do.
Throughout this book, it might help to keep in mind that I am primarily addressing unconscious processes.
The neurons I describe reside mostly in parts of the brain that only indirectly participate in conscious perception.
But they all depend on temporal processing to perform their functions.
Neglect of these billions of neurons has led to experiments and theories that do not capture how the brain processes time.
Daniel Everett argued that the Piraha language lacks words that correspond to concepts that other people take for granted,
and because those words don't exist, the concepts don't exist. They do not use words for colors or numbers, for example,
and do not perceive the world in those terms. On the other hand, they have a rich language in which they discuss their lives in the forest.
Our language for discussing time is impoverished by our conditioned concepts of one-dimensional time.
I discuss throughout this book how to enrich our concepts.
Buzsaki and Tingley argued that neuroscience does not require the concepts of space and time
to make sense of how the brain (at least the part of the brain they considered, the hippocampus and related structures)
performs its computations. Unfortunately, they emphasize that time and space are not represented by the brain.
I would question whether anything is represented in the brain. Instead, I regard brain function in terms of causality.
Neuronal activity causes perceptions, emotions and behavior. And time.
The brain is most often modeled as a hierarchy of areas. The simple notion that most neuroscientists rely on
is that an event in the world causes changes in neuronal activity in one brain area, after a brief latency.
This activity is then conducted to other areas in the brain with an additional delay, and then on to further areas
moving up a hierarchy, with delays between each stage. For this simple notion,
the hierarchy could be defined by the latency of the response in each area, shorter at the bottom of the hierarchy
and increasing proceeding up the hierarchy.
Lots of things are wrong with this hierarchical idea. First, as a general complaint, the concept of a hierarchy
probably occurs to people because we are conditioned to think in these terms.
Military, academic, business, and numerous other social systems are organized hierarchically.
We impose our conditioned concepts on other systems like the brain. This view is contrary to the conventional idea
that hierarchies are essential to the way we think.
Second, brain activity is poorly localized in time. That is, action potentials (also known as spikes5),
the main form of neuronal activity, do not just occur at a moment, and at all other times the neuron is silent.
If you hear a sudden sound, many neurons will suddenly change their activity right after the sound occurs.
But when you hear somebody talking to you, neurons are continually activated, firing action potentials at different rates over time.
The simple notion assumes wrongly that neurons are silent until a stimulus comes along.
My students were taught this lesson by the following exam question.6 You are invited to Dubai to give a talk.
At the end of the day of your presentation, you go back to your hotel, and ascend to your room on the 70th floor.
You are exhausted and get into the shower. As soon as you turn it on, you have hot water. As you relax, you ponder how it is that the hot water comes on so quickly.
The boilers in the basement almost 300 meters below heat the water, and it has to take time to pump that water all the way up.
How is this done?
The lesson is that the water is continuously circulated. Opening a tap simply lets the nearby hot water flow through the local outlet.
The brain similarly circulates activity continuously. Neurons are active much of the time, and what counts is how that activity changes over time.
When something happens, activity increases or decreases, and those changes in signaling drive behaviors.
This makes it hard to measure latency, and to use it for figuring out how the brain works.
We have a geothermal system at home that consists of four 180 foot deep holes,
from which fluid is circulated through a heat pump to cool the house in the summer and heat it in winter.
The pump does not need to work so hard to move the water up the 180 feet, since it circulates with the water that drops 180 feet.
A similar system moves inclines up and down hills (Duquesne Incline).
Another analogy is how electricity flows through wires. Electrons do not travel far, they move somewhat randomly (it's actually
more interesting than that: Quantum effects),
but the very large bulk of electrons shifts in one direction (a bit like Movie 12). In neurons, ions don't so much flow through channels in the membrane,
but, like the electrons, just move microscopic distances to carry the electric current through their distributions on each side of the membrane.
Our intuition is often not helpful at very small or large scales. Like brain activity, charges are poorly localized.
Third, when activity in different parts of the brain is actually measured and latencies are determined,
each area has neurons that respond over a wide range of latencies
(Fig. 2; this is Figure 4 in Nowak and Bullier 1997 that provides far more depth).
These latency ranges overlap across different areas. In other words, all of the areas are firing action potentials at the same time.
Activity does not just propagate up a hierarchy. Nowak and Bullier conclude "Thus, if one assumes that latencies to visual stimuli provide a reasonable estimate
of the order of activation of cortical areas, it appears that the order does not follow the one suggested by the anatomical hierarchy of cortical areas."
We will see that there are properties of the brain that are consistent with a hierarchy,
but need to be careful when modeling the brain. In particular, latency does not provide a useful way to determine a hierarchy.
We will consider whether duration maps into a hierarchy from the back toward the front of the brain.
To get to the heart of how to actually think of time, we measure time based on two dimensions (using Barbour's metaphor, time is dressed in two dimensions):
a series of values ("phases") telling where we are in each of a set of arbitrary periods (e.g., the year, the month, the week, the day, the hour, the minute, the time it takes to get dressed, ...).
Phase and period (or its reciprocal, frequency) are the two dimensions.
Most of the world (we argue that everybody, even though they don't recognize it) uses the two-dimensional view of time. The Mayan calendar (Fig. 3) is one well-known example.
It consists of a large set of periods, with names for the days and months giving the phases.
Despite most people not being explicitly aware of it, we almost always use two-dimensional representations of time.
Our clocks tell us at least two sets of periods and phases, as do our calendars.
The conventional view of time does consider more than latency. Often, duration is measured.
An example is to estimate how long an audible tone is present, as when a musician plays a rhythm with sustained notes of different durations.
We are frequently conscious of durations, growing impatient when something takes longer than we expect, for instance.
Barbour focuses on duration. Although this is an important subject that we will touch on below (the period/frequency dimension becomes important),
our focus will be on timing. To be definite, timing involves when things happen, relative to when other things happen, and is measured mostly by the phase dimension.
Time only exists because we detect changes in the world, because of changes in our brain activity.
These changes can be regarded as generalized motion, the change of some set of neuronal activations, or, in physical terms, changes in the state of the universe.
We will return to the importance of thinking about time in terms of motion.
Motion has two components, speeds and directions. Direction will play the larger role.
The thesis here is:
This treatise will probably appear to be deadly serious. So remember to get your laughs wherever they might be.
Listening to this might help.
Footnotes
1 An obvious resolution to this problem is that a series of events occurred over a long time that resulted in the evolution of birds that laid eggs. And that noon and midnight are series of points on the line.
The point here, as detailed below, is that we often regard noon and midnight as singular events:
the many noons and the many midnights can each represent one thing to us.
Much of what we experience is repeated in a similar fashion over time, and we think of those repeated activities as sharing a single time course.↩
2 Circular reasoning, but the point is that time equals changes in neuronal activity.
This is an issue that is present throughout this book, that I don't reject the word "time" even though I reject a simple interpretation of its referent.
In Philosophy of Language, the usual example is Russell's "The Present King of France."
We understand "time" semantically even though we don't understand what it refers to.↩
3 Parmenides was a 5th century BCE Greek philosopher who lived in Elea, on what is now the Italian coast.
His work is known to us only by a set of fragments written in Epic Hexameter, the style of Homer.
Parmenides' philosophy of Monism, that everything is one, challenged thinkers to falsify his propositions, as he and his pupil Zeno tried to falsify the Milesians' ideas about change.
He got a lot right, including continuity. His monism could be interpreted in terms of things like the "laws of physics" being eternal.↩
4 Abstractions can be regarded as not having existence. Nominalism is a philosophy that rejects abstractions, so that red things exist, but red does not.
Nominalism is discussed further below.
In my second year at Caltech, I was exposed to Linguistics. The professor for this course, Bozena Henisz Dostert Thompson,
spent the first term in her home country of Poland, and her newlywed husband Fred Thompson took over the teaching.
Thompson had diverse training and interests, having studied with logician Alfred Tarski,
and worked in computer science. He developed natural language abilities in computers,
which at the time were not really capable compared to what we have now.
He taught us about Chomsky's theories of grammar,
and I did an independent study with him that I wanted to be about Structuralism,
but he made it primarily a deep dive into Nominalism (Nelson Goodman and Willard Van Orman Quine).
I was slow to appreciate the good parts of Nominalism, but am now committed to avoiding categorization of people.↩
5 One of many beautiful phenomena in the brain, that these types of remarkably complex signals evolved,
with so many accompanying specializations.↩
6 Thanks to Ray and Tom Magliozzi, the car guys.↩
7 Up the hierarchy is defined by projections from a lower area to the middle cortical layer (4) in the upper area.
Projections down the hierarchy go from layer 5 to layer 2/3.↩
When we say what time it is, we provide a series of phase values for several periods.
If it is 10:37 am on Tuesday 10 May 2050,
we mean that it is late morning early in the week about a third of the way through the month almost halfway through the year midway in the century.
These are pairs of values, a phase and a period, for the periods of a day, a week, a month, a year, and a century.
Phase refers to how far around a cycle things lie. We are interested in the set of phase values over a range of periods.
Phase is a property of continuous processes. For discrete situations, in which items can be counted, we learn about doing division,
where remainders are left after dividing one integer by another. For division by 4, the remainders can be 0, 1, 2, or 3.
These remainders are the discrete version of phase. On a clock with 12 hours,
we measure phase over a 12-hour period by saying what hour we are closest to.
On a calendar page, we measure phase by what day it is over a period of a month, for which the period ranges between 28 and 31 days.
The periods we use are somewhat arbitrary, though sometimes derived from some natural phenomena
(the origins of our western units of time go back primarily to the ancient Near East,
developed with the recognition that 12 and 60 have many divisors).
But of course we reckon time in terms of months and years that actually have varying periods.
We might receive paychecks monthly and keep track of payday as a given phase, even though the distance between paydays varies on the timeline.
We rely on the day of the week to organize our lives, even though weeks don't clearly correspond to natural phenomena
(the number of days in a week has varied across cultures). Seconds, minutes, and hours are relatively artificial periods as well
(derived from dividing larger units by factors of 360, i.e. 1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 18, 20, 24, 30, 36, 40, 45, 60, 72, 90, 120, 180, 360).
Ptolemy divided the circle into first and second minutes using successive divisions by 60, giving us what we now term minutes and seconds.
The circle was often divided into 360 degrees, a system that persists for measuring phase.
Phase is also measured relative to 2 times π, as radians, so that halfway around the circle is π and a quarter of the way around is π/2.
I choose to measure phase as the fraction of the way around the circle, so halfway around is ½ and a quarter of the way around is ¼.
The unit of phase is a cycle, so a half cycle and a quarter cycle are sensible quantities.
Remarkably, many people are oblivious to the fact that we divide time into these different periods and the periods into different phases.
One of many examples is the meme that attributes a criticism of the use of Daylight Saving Time to various Native Americans (Fig. 4):
"Only the government would believe that you could cut a foot off the top of a blanket, sew it to the bottom, and have a longer blanket."
The notion that the day resembles the progression from the top to the bottom of a blanket, and, worse,
that days don't change their behaviors over the course of a year with different seasons,
seems more likely to arise from a modern urbanite in less touch with nature than at least the stereotype of Native Americans.
For most of human history, the earth's rotation was the primary source for measuring time, based on the movement of the sun across the sky during daylight,
and the stars at night. Dividing daylight into 12 hours and the dark phase of the day into another 12 hours requires those hours to vary across space and time,
because these periods change with the seasons and latitude. However, for most purposes, these approximate phases of the day worked well and were useful.
Daylight savings time resets phase in a relatively crude way by jumping by one hour twice a year. We could instead just shift by about 20 seconds every day,
or smaller amounts every hour (about 1 second) or minute (1/60 of a second) or second (1/3600 of a second).
Those adjustments would have their own problems, of course,
because of our technological world that requires lots of synchronization, but might be managed by that technology as well.
We would not be aware of these miniscule resettings of phase.
Phase is a relative quantity. In physics, everything is relative. The same is true in biology
(and geology, chemistry, sociology, anthropology, …),
and we emphasize that phase is the right way to think of biological processes.
Cell division is characterized by a series of phases, for one example.
These phases can take variable durations, but the sequence of events happens predictably: G1, S, G2, and M phases.
Time itself is of course relative.
We discuss phase and period in terms of timing and duration. Phase describes the relative timing between processes,
and period describes the duration being looked at. Phase is usually a function of period.
Two processes differ in their timing based on the phase difference between them at each period.
Lunch and supper differ in their phases at a period of a day. Over a period of an hour,
they may have similar phases in how we go about eating each meal.
Over the duration of two related processes, this behavior of having similar phases might be expected.
Over other periods, phases are expected to differ.
Thus, duration (period or frequency) and phase are two ways of describing time,
and together they capture how things change in time.
We use phase values at a series of periods to tell time, and so does the brain, as explained further below.
Computers, on the other hand, internally count the number of some very short periods, "ticks", since some fairly arbitrary moment.
My computer tells me that it's been 3776668273 seconds since midnight 1 January 1904.
We certainly do not get much information from that sort of time value. But computers do the arithmetic to translate between ticks and the phase values over periods we understand.
It is instructive to consider how we can perform such translations. We can set up rules to take any two dates and estimate the number of seconds between them.
Those rules can be a bit complicated because of the variability in the periods we use. But if we rely only on fixed periods,
we can easily compute the time between two dates, using the Chinese Remainder Theorem.9
Imagine that you are the Emperor, and want to count how many soldiers you have in your army. You stand on top of a mountain looking down on your troops,
and direct your generals to have the soldiers organize themselves into small groups of 3. They do so easily by shifting their positions a little bit.
But one soldier is left over at the end, the remainder of your desired number after dividing by 3.
You then direct them to form groups of 7. They do so, and you write down that there were 6 soldiers remaining.
You do the same with groups of 17 and 29, finding remainders of 5 and 2.
From those quick manipulations, you can determine the total number of troops, in this case 9253.
This result generalizes. We can do the same thing for data that aren't discrete, using continuous phase and frequency values.
The slope of phase vs. temporal frequency is latency. This is best appreciated by knowing a basic property of Fourier transforms:
f(t-L) ⇔ e2πiLω F(ω)
When people think of latency in the one-dimensional time domain, they generally rely on picking particular moments in time.
These choices do not necessarily reflect the underlying functions (e.g., stimulus and response,
neither of which is typically a "delta" function, infinitely narrow and tall, completely localized in time).
The choices of moments might just be onsets or peaks of those stimulus and response functions, for example.
Because of these choices, that sort of time-domain definition of latency is notoriously unreliable.
In contrast, the definition used here, the slope of phase vs. frequency, is precise, accurate,
and generally applicable, as it is based on the equivalence above.
The addition of integer numbers of cycles to the phase values as described above is not as ill-defined as it might seem.
For our purposes, phase is measured at each of a series of temporal frequencies that are spaced closely enough together
that neighboring phase values are separated by less than a cycle.
The only manipulation that is needed is to ensure that the phase values are slowly increasing as a function of temporal frequency
(e.g., the "unwrap" operation in Igor).
Another way to understand that latency is the slope of phase vs. frequency is to think about what latency does.
If some process responds with a fixed latency to an input, when does the response occur at different frequencies?
Let's take an example where the latency is 100 milliseconds (100 ms). At a frequency of 1 cycle/second
(1 Hz), 100 ms is a tenth of a cycle (0.1 c).
At 2 Hz, one cycle takes half a second, 500 ms, so 100 ms is 1/5 c = 0.2 c.
At 5 Hz, one cycle is 200 ms, so 100 ms is 0.5 c.
At 10 Hz, one cycle is 100 ms, so the phase is 1 c.
If you plot these phase values (0.1, 0.2, 0.5, 1)
against these frequencies (1, 2, 5, 10),
you get a line where phase (in cycles) = 0.1 (s) * frequency (Hz). The slope of the line is 0.1 s = 100 ms.
As frequency gets higher, the period gets shorter, and a latency takes up a longer portion of a cycle.
This hopefully makes it clear that latency is exactly the slope of phase vs. frequency.
This relation can be written as φ=Lω, phase is the product of latency and temporal frequency,
ignoring momentarily what will be explained next.
In the typical experiment where a stimulus evokes a response, both the stimulus and response are extended in time.
The poor localization in time makes it difficult to work in the time domain, but working in the frequency domain,
as we will explain with numerous examples below, facilitates both execution and analyses of experiments.
In the frequency domain, one measures both amplitude and phase as functions of frequency.
Amplitudes typically grow weak at low (too slow) and high (too fast) frequencies.
For our prime interest in timing, phase is more important than amplitude.
As above, phase values increase with frequency, with the slope giving the latency.
The key parameter that describes timing, however, is the intercept of the phase vs. frequency line, the phase at 0 Hz.
Note that this can not be directly measured, since a single cycle at 0 Hz lasts forever,
but is instead extrapolated from the data at low but non-zero frequencies.
Thus, the line that plots phase vs. temporal frequency is φ=Lω+φ0,
where φ0 is the phase at 0 Hz.11
The phase at 0 Hz, what we call absolute phase (analogous to the temperature of absolute zero,
which can not be reached but can be extrapolated as approximately -273°C;
the term is an oxymoron, given that phase is relative), describes the shape of a function of time.
Phase is by definition a relative quantity, and we use a convention where phase is measured in cycles,
with 0 cycles corresponding to the peak of an even (symmetric with respect to time, after accounting for latency) function,
and +0.25 cycles corresponding to an odd (antisymmetric) function with a negative phase preceding its opposing positive phase (Figure 6, black and red curves).
Absolute phase values of 0.5 c and -0.25 c correspond to shifting the black and red functions by a half cycle, giving the blue and green traces.
Absolute phase values just less than 0 c are termed phase leads; phase lags correspond to absolute phase values just above 0 c.
These terms apply to functions with phase values around 0.5 c as well, so that an absolute phase value of 0.4 c is a phase lead.
In the visual system, illustrated with examples below, neurons that respond with phase values around 0 c are called ON-center,
and those with phase values around 0.5 c are called OFF-center.
This is a somewhat unfortunate terminology originating with early studies where only bright stimuli could be easily generated,
so cells that are excited by dark stimuli were tested by turning off the bright stimulus.
Our goal is to characterize how the brain transforms external sensory stimuli into neuronal activity.
These characterizations are simplified by thinking in terms of frequency, amplitude, and phase.
In the frequency domain, any stimulus and any response (at least, that we can generate and measure! -
formally, members of the ℒ2 function space, "square-integrable" functions)
can be characterized in terms of amplitude and phase as functions of frequency.
The system (e.g., the brain) that turns the stimulus into the response is analyzed by correlating the stimulus and the response.
In the time domain, that correlation is a slightly complicated process termed "convolution" (it's convoluted!).
In the frequency domain, it is simply division of the response by the stimulus.
Formally, this is division of complex numbers, but in terms of the real components of amplitude and phase,
it is division of amplitudes and subtraction of phases. The result of this analysis is called a transfer function,
or a kernel, among many names. We will refer to kernels, in both time and frequency domains.
The phase of the kernel is thus the difference of response minus stimulus phases.
The brain or other system changes the stimulus phase into the response phase, and the kernel describes this change.
We model this process in terms of the response R arising from the stimulus S via the kernel K:
So time is two-dimensional, with one dimension being temporal frequency, and the other phase.
A standard way to think about the two-dimensional space of time is as a disk, with the center point missing (Figure 14).
The distance out from the center is frequency or period, and the distance around the disk along any fixed frequency is phase.
This representation of time is clearly different from the time line!
We are quite familiar with such representations of time. Our clocks tell us what time it is by giving us phase values for some small number of periods.
Analog clocks are versions of the disk, usually showing the hour (the phase over a 12 or 24 hour period) with a short hand,
and the minute (phase over a 1 hour period) with a longer hand, farther out on the disk - so the opposite direction from the center compared with Fig. 14,
where longer periods are farther out.
On our calendars, weeks are laid out, containing 7 days. Some of our activities are centered on certain days,
and thus can be considered as having different absolute phase values. Maybe we tend to eat tacos on Tuesdays,
and worship on Fridays, Saturdays, or Sundays, structuring our behaviors around different positions in the week.
We will see that absolute phase in a neuron corresponds to the timing relative to some phase of the process that affects the neuron,
so that the neuron anticipates, goes along with, or follows behind the timing of the process.
These different neuronal timings combine to provide us with the directions in which things change.
Neuroscientist Dean Buonomano's excellent book
Your Brain is a Time Machine describes many of the phenomena we treat, but he relies on one-dimensional time.
I don't mean to criticize him personally, but think his book makes a fine example of how treating time as two-dimensional gives us more insight.
His emphasis on moments of time leads to all sorts of problems. What's more, he barely touches on direction.
He argues that time is more complicated than space.
Because rodents have neurons called "place cells" that are active when an animal passes through a certain region of their environment,
he claims that their brains have a spatial map. He almost gets it right by noting that their mapping strategy is more flexible than GPS.
A rat that is trained to run down a track will have place cells that are active at different positions along the track;
if you block the track halfway along, the neurons adjust to the new length.
This is to be expected if you realize that the neurons care about the spatial phase along the track.
All of our neurons care about phase, and time is not so complicated when thought of in its natural two dimensions.
Buonomano continues by noting that we can navigate through space but not time.
We will discuss at length how temporal phase gives us the sense of where we are in whatever processes we're involved in.
What counts is that we know whether we're at the beginning, middle, or end (or anywhere in between) of what we're doing.
If we want to restart at the beginning after we've gotten to the middle, we can!
We are able to perform complex tasks in the correct order because we "know" where we are in time, and importantly, where we've been and where we're going.
We are simply misled by the unfortunate conditioning we've undergone claiming that time is one-dimensional.
He notes that we use modular arithmetic (meaning remainders, which is the discrete version of phase) to tell time,
and states that is confusing, especially to children.
He relies on Piaget's studies of how children process time.
What Piaget showed was that children internalize time in terms of the processes that they're involved in.
This intuitive time is exactly how we use time when we're not trapped by the delusion of moments.
Perhaps before we're conditioned to think in terms of the timeline.
We will discuss how time interacts with other dimensions such as space, odor, happiness, and everything else that concerns us,
to provide the information we need for all of our behaviors. What we need to know is how things are changing in time,
and how to make our bodies and the external world change in time. The key notion we emphasize is direction.
Buonomano also has a great summary of work on timing in fruit flies that was carried out by Seymour Benzer and colleagues.
He made an understandable error in claiming that Benzer was a Nobel laureate, whereas he was famously never awarded that particular prize
(Benzer's mother complained that was the only thing her neighbors cared about).
Max Delbrück was instrumental in Benzer's work. They were founders of molecular biology, and in particular how genes affect behavior.
Benzer mutated genes in fruit flies and then cleverly tested the flies to reveal behavioral changes.
His lab identified hundreds of such mutants. A few of the best-known examples have to do with circadian rhythms.
In fruit flies, Benzer could characterize the way cells signal the time of day. The mechanisms behind these cellular clocks are now well-described.
Thinking of the brain as a clock, or really many billions of clocks, we will now describe how neurons tell time.
These cells provide timing information as phase values across a range of temporal frequencies, as do clocks.
Neurons typically produce signals consisting of action potentials, also known as spikes.
These are voltage changes on the time scale of about a millisecond. But little of our behavior happens on that time scale,
so neurons signal by generating series of spikes, often termed spike trains.
A popular idea about what is important about a spike train is that the firing rate,
how many spikes are generated in a given period of time, determines the function of the neuron.
If a neuron fires at 100 spikes per second, it can strongly influence neurons to which it communicates.
But absolute firing rates vary tremendously across the nervous system, so in some neurons,
firing rates of only a few spikes per second can be effective.
What counts is when firing rates go up and down.
That is, what matters is that firing rates vary over time. Consider a neuron that cares about light inputs to the retina.
If light reaching the eye varies in its luminance over time, the neuron's activity is likely to be modulated in time by the stimulus.
An example is illustrated by Movie 2. The stimulus is a small spot, and the luminance changes over time in a 4-part sequence,
from dark to background to bright to background and back to dark.
The movie shows several cycles of the stimulus, and the audio lets you hear when spikes occur during the stimulus presentation.
Firing rate increases around the times when luminance increases, either from the dark to bright transition or from the background to bright change.
Averaging across many cycles of the stimulus, we show how firing rate
(in impulses per second, "ips", the same as spikes per second) depends on the stimulus (Figure 7).
Three neurons illustrate how there is a range of timing. The transient nonlagged cell (1) at the top
responded primarily just at the luminance increases, after 0.5 and 1.5 seconds.
The sustained nonlagged cell (2) also fired at those points, but continued to fire as long as the spot was bright.
The transient lagged cell (3) did not fire at the stimulus onsets, but was active during the period when the spot was bright,
then fired strongly at offset (2.5 s).
This response lags the stimulus, therefore.
The terms transient and sustained have been applied to certain visual neurons since the early 1970s
(Cleland et al. 1971).
Related terms like phasic and tonic are also used.
The term lagged, on the other hand, originates in this context from
Mastronarde 1987.
The most important note is that these terms refer to temporal differences. That fact has often not been appreciated.
Keep in mind that just as many OFF cells exist that fire a half-cycle away from these ON responses,
showing responses similar to these cells but to a stimulus that turns dark rather than bright.
The distinction between ON and OFF cells becomes slightly less important when thinking of two-dimensional time,
but is biologically rooted in the
retinal mechanisms that produce them.
Different cells respond at all of the phases around the cycle (Fig. 9).
ON cells have absolute phase near 0 c, between -0.25 c and +0.25 c,
OFF cells near 0.5 c, between +0.25 c and +0.75 c
(note again that adding an integer number of cycles to a phase value does not change it,
so -0.75 c to -0.25 c is an equivalent range for OFF cells).
Cells in the quadrants between 0 and 0.25 c or between 0.5 and 0.75 c are called lagged cells,
and those in the other two quadrants are called nonlagged cells, roughly speaking.
As noted above, transient cells have absolute phase approaching ±0.25 c,
and sustained cells have absolute phase near 0 or 0.5 c.
An important concept, really the primary concept, in sensory physiology, is the "receptive field" of a neuron.
The receptive field can be defined broadly to be the set of stimuli that modulate the neuron's activity.
Often, the term is applied to the spatial receptive field, the region in space where stimulation can affect the neuron's firing.
But we will focus largely on the temporal receptive field. This concept is less familiar.
It can be considered to refer to how the neuron turns stimulus timing into response timing (the temporal kernel).
The time domain temporal kernels, also known as impulse response functions, are shown in Fig. 10 for the 3 cells in Figs. 7 and 8.
These are like the traces in Fig. 6 (green, black, and red). This representation of temporal receptive fields is conventional.
Unfortunately, quantifying the differences between these three examples in the time domain is challenging.
However, they are easily described in terms of phase values.
The Fourier transforms of the functions shown in Fig. 10 provide amplitude and phase vs. frequency from which one obtains absolute phase and latency.
More examples of how absolute phase corresponds to response timing are available
(e.g., Figure 11 in Saul and Humphrey 1990;
Figure 9 in Saul 2008;
and Figures 2 and 3 in Saul et al 2005).
Figure 11 shows the temporal receptive fields of two kitten LGN neurons.
The cell on the left is transient nonlagged, with an absolute phase of about -0.2 c.
Its temporal receptive field therefore lies about 80% of the way to the downward axis at low frequencies.
The transient lagged cell on the right has an absolute phase of about 0.2 c, so starts about 80% of the way to the upward axis.
They are about a quarter cycle apart at 0.5-4 Hz. By 6-8 Hz (portions within the 4 Hz circle), they have similar phase values.
The latencies differ considerably, with the nonlagged cell completing more than 1 c
while the lagged cell doesn't pass through a single cycle over about 8 Hz,
as can be seen in the temporal receptive field plots.
People often ignore what they consider to be messiness in order to supposedly simplify their thinking,
for instance by considering race to be meaningful, or by deciding which sports team or athlete is #1.
We tend to impose artificial thresholds in order to create discontinuities where there are none:
if team A beats team B, A is thought to be clearly superior to B, even though if they played multiple times
they would each win some and lose some, and in reality are probably similar in capabilities.
Whether this tendency to categorize corresponds to the way the brain works innately,
perhaps a property of associative memory,
or comes about through cultural conditioning, remains unclear.
It may be an adaptation for making decisions rapidly,
similar to beliefs. We are nonetheless quite capable of relying on continuous, fuzzy, phase-based information and actions.
Consider the very important topic of moods. We sometimes pretend that sadness and happiness are discrete,
but we know that our sadness can vary, from the sorts of devastation we feel when we lose a loved one,
to when we hear about the death of somebody we don't know, to when we lose a game.
Our moods obviously change over time, often at a very slow pace, but occasionally rapidly.
These changes in mood motivate much of our behavior.
Our goal is to understand some of the neural mechanisms underlying these functions.
Wang and colleagues 2011
recorded from neurons in the mouse amygdala,
a brain region that is important for emotional processing.
They found that many neurons fired in relation to the anxiety of the mice.
Figure 12 illustrates some of their results.
This is direct evidence that single neurons can show slowly modulated activity,
with phase values that correspond to highly sustained and lagged patterns.
This must be true if you accept that single neurons underlie our behaviors,
but it could be that only activity across populations of neurons would show this.
The transient, sustained, and lagged kitten LGN neurons illustrated above provide an example of how certain human behaviors might be created.
Tallal 1980
studied a common problem seen in 5-10% of children entering primary school.
These children had difficulties that people thought were due to defects in how they processed language.
Tallal and colleagues demonstrated that the defect appears to lie at a low level, and is specific to temporal processing.
These children have deficiencies in processing rapid changes in any modality (auditory, visual, tactile, motor, ...).
I would characterize this as a deficit in transient neural mechanisms,
those that respond best as things are changing rapidly, with a phase that leads the input by about a quarter cycle.
Our speculation is that the neural substrate lies in thalamus, a part of the brain through which almost all inputs to cortex pass, covering all modalities.
The main visual thalamic nucleus is the LGN. Neurons in thalamus vary in their timing, as described above and discussed further below.
Disruption of transient timing in thalamus could produce the problems seen in the children studied by Tallal.
Paula Tallal tells a story about when she would go to children's homes to try to help them.
The project used synthesized speech that slowed down the rapid changes in sounds that distinguish consonants like /ba/ and /da/ (Figure 36).
The children would put on headphones to listen to a story generated with the synthesized speech, while playing a video game related to the story.
The affected children would enjoy the story, being able to finally understand what was being said.
The unaffected siblings, on the other hand, would hate listening to the odd speech and would take off the headphones in disgust.
Another large group of children (as well as adults) have attention deficit hyperactivity disorder (ADHD).
This disorder may correspond to a deficit in sustained and lagged mechanisms in thalamus, with phase values near and greater than 0.
Those neurons might be important in sustaining attention, for instance.
They could also play an important role in reinforced learning, as detailed below.
Besides these disorders, processing of time varies across human populations without being considered pathological.
We know some people who are always late. If they need to be somewhere by noon, they only start getting ready at noon.
We speculate that they lack transient neurons that respond ahead of stimuli, with phase leads.
Other people tend to do things ahead of time, getting prepared in advance, getting to appointments early, etc.
They may have an abundance of transient neurons.
It may be difficult to understand this in terms of points on a line, but easy when considering deficits in sustained and transient phase processing.
A misconception that is worth addressing is that many people think analysis in the frequency domain somehow applies only to periodic functions.
This is far from the truth. As noted above, any reasonable function can be examined in the frequency domain,
technically the "square integrable" functions that are mainly characterized by having non-zero amplitudes that don't extend out to infinity in time,
so the amplitude goes to zero at low temporal frequencies. For our purposes, there is nothing about the work described here that entails periodic changes in any variable.
Keep in mind that the description of a function in the frequency domain consists of amplitude and phase across the entire range of frequencies.
Periodic functions are simply those where the amplitude is zero over all but a finite subset of those frequencies.
Absolute phase and latency are weakly correlated with the temporal frequency tuning of amplitude.
Lagged cells tend to be tuned to slightly lower frequencies than at least transient nonlagged cells.
The underlying reason might be that cells with longer latencies (Figure 31)
can not respond well at high frequencies simply because their latencies approach and exceed the stimulus periods at those frequencies.
A neuron with a latency of 100 ms can not respond well above 10 Hz (period of 100 ms).
Readers will probably think that much of brain function happens in moments, rather than extended periods of time.
Changes in the external world happen mostly over long time scales. Our internal thoughts and emotions are similarly slow.
Most experiments demand fairly isolated processing. In the real world, we must deal with numerous distractors.
We often need to search through activity that is filtered out as irrelevant before we get to the task at hand.
Because most things change slowly in time, we are less aware of all the things going on at low temporal frequencies,
to which we slowly adapt (see below; Cohen room).
Many authors continue to disregard phase, and write that
different latencies across a population of neurons could be the basis of direction selectivity.
We will discuss this issue at length, emphasizing that direction selectivity varies with temporal frequency due to the interaction of absolute phase and latency.
We concentrate on time here, but must mention that space should be conceived in an analogous fashion.
We don't say where we are in GPS terms.
We describe our location in relative terms. We live on the south side of town,
and at the current time are upstairs in the middle of the study at the front of the house.
The moon is low in the sky above the tree at the edge of the yard. The brain similarly uses phase to locate us in space.
The hippocampal place cells mentioned above are created from two-dimensional spatial maps in entorhinal cortex.
The entorhinal neurons were termed grid cells.
There are grid cells with different spatial frequencies and phases, mapped across entorhinal cortex.
Elsewhere in the brain, there may be many other spatial mapping strategies, but it's a solid bet that they rely on frequency and phase, just like time.
Our view of time differs from the conventional view. We will now make this more precise,
by describing some mathematical structures that will be relevant for understanding how the brain processes time.
A topological space is a set of points and a set of subsets of those points (called the open sets) that satisfy a few conditions:
the empty set (with no points in it) and the entire set are open sets; any finite intersection of open sets is open;
and any union of open sets, even of an infinite number of open sets, is open.
That is, the set of open sets is closed under finite intersections and all unions (Figure 13).
Our point of view is that moments, corresponding to points on the line, do not exist.
Instead, the basic objects of time have extension, and correspond to open sets in two-dimensional time.
Things happen over these open sets, and processes have non-zero durations.
Thus, thinking about the topology of time, we ask what points in time are near each other.
Many people would say that times that are separated by any arbitrary short length of time are near each other,
thereby thinking in terms of the natural topology on the line.
The notion of continuity will arise below, but we won't go into its technicalities.
The key idea is that we think of time in terms of our activities. If we say that it's time to eat lunch (dinner for some people),
sets of times that might be roughly repeated every day are thought of as near each other.
These points form an open set on the line, but it is natural to think of them on the disk,
where a period of a day is a circle that lies at a certain distance from the origin, and lunchtime takes up a small segment of the day.
Note that I've chosen examples of phase values that are easy to understand in terms of fairly natural periods,
especially of one day. This is by no means necessary, it is simply a choice to try to make the explanations simpler.
The disk of time (Figure 14) consists of the set of all periods and phases, with periods positive (greater than 0) real numbers,
and phases having values between 0 and 1,
with 0 and 1 being the same point (so phase takes values on a circle). The disk is the product of the open interval of real values greater than 0, times the circle.
The periods should be plotted logarithmically, so that the distance between a second and a minute (a factor of 60) is the same distance as between a minute and an hour.
One can also think of this as a cone, which may give a better picture of increasing periods with distance from the apex of the cone.
When we walk, we move one leg forward, then bring the other forward, no matter how fast we walk.
This makes sense when thought of in terms of the phases at which different behaviors occur over some periods.
We don't move the right leg forward at a fixed number of seconds after the left leg: that depends on how fast we're walking.
But we generally move our legs in fixed phase relationships. When dancing with a partner, this is usually necessary!
We can map points on the line to the disk, and vice versa. It should be obvious, however,
that these representations of time are different from each other.
For instance, the disk and the cone are equivalent topological spaces, as are the subset of the line between 0 and 1 and the entire line.
Intuitively, two spaces are equivalent if they can be continuously deformed into each other.
The line can not be continuously deformed into the disk.
The most obvious difference between the disk and the line is their dimensionality. As mentioned above, that time is two-dimensional might not seem apparent to people who are heavily tied to the one-dimensional view,
but all of our normal time-keeping is done with two-dimensional displays: calendars showing several weeks and days in each week, clocks with hands showing the phase for at least two periods,
and even digital displays showing the hour, followed typically by a colon to separate that phase from the phase given as the number of minutes in the hour.
Note that a sundial is really one-dimensional, with the topology of the circle: only a single period is displayed, so that the period dimension collapses to a point, a zero-dimensional space.
A single point on the line projects to a set of points on the disk (Movie 4) that form a spiral.
These points all have phases near 0 for long enough periods (periods much longer than the value of the time).
With decreasing period, phase increases. The relation between period, phase and time is t=𝜑⋅pd,
where t is the time, 𝜑 is the phase, and pd is the period.
This relation can also be written as 𝜑 = ωt, where ω is temporal frequency, the reciprocal of period, as pointed out above,
where we discussed that latency (the variable t here) is the slope of phase vs. frequency.
The power of the frequency domain view of time lies in putting together different processes to see how they might be related.
If you want to see how the attention paid to the meeting is related to some other variable, such as release of a stress hormone,
alertness, sympathetic activation, or dopamine release,
you could convolve the rather complicated time-domain function above with a similarly complicated time domain function for your other variable.
Such comparisons on the time line are difficult to quantify. In the frequency domain, on the other hand,
it is mostly a matter of dividing the amplitudes and subtracting the phases between the two functions.
The phase difference tells you how your variables are related: what direction and timing any causal relationship might have.
The sign of the latency gives the direction of causality.
An absolute phase difference near 0 means that your variables are synchronized,
but other absolute phase values give insights into the transformations going on between them.
A function in the frequency domain defines a contour above the disk, with the height being the amplitude,
typically lying along a spiral (𝜑 = Lω + 𝜑0).
Over the range of frequencies where two functions have strong amplitudes,
the differences in the slopes and in the phases at low frequencies determine the relationship between them.
Although the amplitudes contain information that can be important,
the key information lies on the disk, in these differences between the phase vs. temporal frequency information.
That is, the kernel or transfer function that relates the two functions is largely defined as a set of points on the disk
where amplitudes are significant.
It is therefore worthwhile to study the category of functions on the disk.
People are taught about the time line for some good reasons, despite its dangers.
The line can in fact be usefully combined with the disk.
This time-temporal frequency hybrid can take the form of a wavelet transform from the time domain to this time-temporal frequency domain.
The wavelet representation derived from a function of time shows the amplitude and phase of the original function
as a function of frequency over localized regions of one-dimensional time.
One example of how wavelets can provide additional information involves non-stationary processes.
Imagine that you want to understand the relationships between the function showing your attention on a meeting
and a function showing dopamine release over the same time period.
Say that dopamine release tends to be suppressed until after the meeting because of other factors than purely your attention to the meeting.
It is therefore worthwhile to partition your functions into before and after the meeting.
The wavelet versions are suited to these sorts of choices about portions of time where the system might differ because of other factors.
For instance, you may do the same sort of thing every day, like working. If you want to study some aspect of your work life,
you can focus on a daily period and look at the phase behavior over that period.
However, you realize that the results would be skewed if you included days when you didn't work.
So it is worth cutting out those days from your data set.
A real example of treating a non-stationary system that way comes from
a study of how visual neurons behave with respect to eye movements.
Monkeys were trained to fix their eyes on a small LED for 5 s at a time. While they were fixating,
visual stimuli were shown away from the LED to evoke activity from a neuron in the lateral geniculate nucleus (LGN) in the thalamus.
These neurons have relatively uncomplicated receptive fields (see below),
with a small region in visual space (spatial receptive field) where they respond with particular temporal profiles (temporal receptive field).
Even while fixating, monkeys (and humans) make small eye movements, typically 1-4 times each second.
We don't notice these fixational saccades (jumps in eye position) despite the fact that they make the world jump around on our retina,
like a film shot by an unsteady hand-held camera. One of the questions posed by this study involves how our brains discount these movements so that we don't notice them.
The hypothesis was that these LGN cells changed their behavior around the times when fixational saccades occur,
so that their timing compensates for the jump across the retina.
Through some complicated analyses, including breaking wavelets up into different temporal epochs relative to when saccades occurred,
we determined that the neurons changed their behavior around the times of the fixational eye movements.
There is a considerable literature about what happens around saccadic eye movements.
The main result has been that amplitudes of neuronal responses to visual stimuli are greatly reduced around the times of saccades.
An interpretation is that we are effectively blinded for a brief time, which may be why we don't notice the shift in the world.
Timing has rarely been considered. We showed that a consistent change in timing as well as amplitude occurs for these small fixational saccades.
Absolute phase increases during the period from about 100 ms before to 100 ms after the saccades
(Fig. 18B; this is the same time course during which amplitudes decline).
This makes responses more sustained. Latency shortens remarkably before the saccades, most strongly about 70 ms beforehand (Fig. 18C).
Another problem involves integrating stimulus locations before and after saccades. In the absence of a saccade,
if a stimulus moves abruptly from one spatial location to another, we notice the change.
If the same change in retinal location is created by a saccade, however, we do not see it as movement of the stimulus in the world.
In the first of these situations, only the stimulus moves, and the background of the world stays put on the retina,
whereas in the second case, both the stimulus and background move.
Note, however, that the changes in neuronal receptive field properties occur before the saccade, so do not depend solely on the relative movement of figure and ground.
The solution could be that the timing changes in the LGN that make neurons more sustained permit cells that were responding to the stimulus prior to the saccade to continue their activity after the saccade,
when other cells that have receptive fields at the new location after the saccade are firing.
The overlapping activity in these cells with different spatial receptive fields on the retina could signal that these locations are equivalent in visual space.
Morrone and colleagues performed related psychophysical experiments on humans (Figure 18).
They flashed a pair of bars at different intervals of time between the flashes,
and in either order (bar A then bar B, or bar B then bar A). They also had the subjects make saccades at different times around the flashes.
In one of their experiments, the subject reported which bar came first.
They obtained a compelling result: when the flashes came fairly close together and about 70 ms before a saccade,
the subjects reliably reported the order wrongly. That is, people consistently say that bar B flashed before bar A when in fact the reverse was true.
The interpretation is that time reverses for us just before we make saccades.
In the Saul study, we noted a sudden,
short duration decrease in latency for the LGN cells at 70 ms before the saccades (Fig. 18C).
We speculate that the Morrone results could be interpreted in terms of this change in latency:
if the first bar flashes 100 ms before the saccade, it would evoke responses at a longer latency than a second bar that flashes at 70 ms before the saccade,
where latencies are greatly shortened. The response to the second bar would then occur before the response to the first bar.
Remember that the responses measured from the neurons in this study were not localized in time.
The analyses needed to be performed in the frequency domain, based on phase in particular.
Working in the time domain alone would not enable these results to be observed.
8 I was teaching calculus to engineering students at West Virginia University, and noticed that a book had been left behind by the previous teacher.
After class, I went to return the book to that professor, but first scanned its content. It was The Geometry of Biological Time, by Art Winfree, a beautiful book in every way.
I found the owner, Ken Showalter, in the Chemistry Department. Ken is a physical chemist, and we wound up talking about the book and many other things.
And wound up collaborating, studying time. I got to spend some wonderful time with the polymath Winfree in the June snow of Utah.
At the time, Ken was working on a chemical reaction that involved the reagents sodium iodate and arsenous acid.
If you put these chemicals in a jar at the beginning of a lecture, they will sit as a transparent liquid.
At some point during the lecture, the fluid in the undisturbed beaker will suddenly turn black.
This is an example of a
clock reaction.
Inorganic chemicals can undergo reactions at regular or irregular times.
Ken had been looking at how the reaction in a tube of this solution can be triggered at one point in space,
creating a wave that traveled down the tube. We worked on analyzing these propagating waves.
I was living on a piece of land we called "Out Yonder" an hour's drive from Morgantown at the time,
working in the woods, cooling off in the pond, then trying to figure out how the waves worked.
Ken and I sent notes (a few years later there would have been email) back and forth about our progress.
He was sorting out the chemistry, and I was playing with the math.
We each came up with the answers from our two perspectives at the same time.
I had seen that the waves could be described in a pretty (closed-form,
meaning easy to write down and read) function if the reaction was a cubic function of iodide concentration.
Ken had seen that the reaction was in fact a cubic. We nailed down how well the predictions fit the data,
determining the speed at which the waves traveled,
and published a paper with Adel Hanna.
That got me started on thinking about time.
I learned many things from Ken, especially about the wonders of collaboration.
Some people don't recognize that Science is about people. But humans are social animals,
and we thrive on our interactions.
The pleasure of doing Science is largely spending time with people you enjoy and appreciate.
Every once in a while you learn something, providing enormous pleasure.
↩
9 My friend Robert Tajima and I took Max Delbrück's course that covered a variety of biological and philosophical topics, including the Chinese Remainder Theorem.
I got to know Max on annual trips to Joshua Tree, with his wife Manny and their children (Tobi works on electronic chips that process visual stimuli,
including direction selective elements that analyze moving images, unfortunately using 1-dimensional time;
Ludina Delbrück Sallam is an Arabic translator; there were two older children I didn't know),
English professors David and Annette Smith's family, and several other undergraduates.
Max kept star charts like the ancients. My last year, he told me how his retinal detachments kept him from being able to make out the stars well enough to continue this work,
and asked if I'd take over his charts. I stupidly declined, fearing I wouldn't do it justice.
Max viewed Science not as building a cathedral, but instead
people piling up stones.
I found his attitudes refreshing and on point.
Max deserved every honor possible, just a giant of a man.↩
10 The right hand side is the Fourier transform of the left hand side here (and the left hand side is the inverse Fourier transform of the right hand side).
The factor that multiplies F(ω) simply produces a phase shift of Lω, so that the latency shift L on the left hand side results in a phase shift of Lω.
The relation between the phase shift and ω is therefore linear with a slope of L.↩
11 Phase is usually not exactly linearly related to frequency, because of linear and nonlinear filtering.
We ignore those complications for simplicity. For most processes, a linear relation between phase and frequency dominates.
This is especially true if amplitude is taken into account,
so that weaker amplitudes are discounted when considering the phase vs. frequency relation.↩
This is one of the biggest problems in neuroscience, as well as elsewhere, the local-global transformation.
Something happens at one time, and something else happens at another time.
How do we know whether or not these things are related, and how do we put them together into a properly ordered sequence?
When we listen to music, we need to integrate hundreds of elements over time,
and we can manage to extract meaning from the total that is clearly not present in any of the parts (Hasson et al. 2008;
Carvalho & Kriegeskorte 2008).
Uri Hasson has explored these issues extensively in several modalities. Note that those studies argue for hierarchical processing.
Almost all functional studies of neurons have considered their local properties, those confined to their limited receptive or movement fields.
For example, visual and somatosensory neurons have spatial receptive fields, the region of visual space or skin where stimulation affects the neuron,
but our perceptions consist of objects that we see or feel.
Motor neurons typically cause a small group of muscle fibers to contract,
but the brain develops networks that plan and execute complex behaviors that employ those simpler motor neurons.
To reiterate the idea presented above, sensory neurons can be thought of as having temporal receptive fields
in the sense of responding at certain phases in the variation of some response property over some range of temporal frequencies.
Different neurons with different temporal phases and different response properties provide inputs to other neurons,
that integrate those inputs to create an emergent response property not present in the inputs.
Motor neurons have movement fields, defined as the movements that the body makes when they are activated.
Single motor neurons are typically local units, but are assembled into more global units in order to execute useful behaviors.
Over the disk of time, a behavior consists of many motor neuron activations that have different phases and combine together to achieve a smooth, accurate movement.
The convergence of these inputs can be thought of as a stitch between them, creating a result that is less local and more global.
One can think of patches of fabric floating above the disk of time, and the brain sews the patches together to produce a larger quilt.
One imagines that there are advantages in creating a smooth, continuous quilt rather than a messy, torn quilt.
Mechanisms for resolving discontinuities are therefore called for, and studying continuity is worthwhile.
We will venture into some abstract mathematics at this point. That will no doubt scare off many readers.
I would urge you to hang on a bit. Hopefully, you will get something out of this. Eugenia Chang provides examples of
how abstract mathematics describes things that we can understand intuitively in her book Unequal
( factors of 30).
The same object does not look the same from different angles, as in the example of the photo of the impossible triangle above.
In general equality and inequality are more complicated than we might expect.
These somewhat vague ideas can be formalized and made more rigorous, via the mathematical field of sheaf theory.
A sheaf is a mathematical object defined as a set of structures called stalks, and a map from the stalks to an underlying topological space.
That map simply says where each stalk is located in the topological space. The stalks can be any sort of object that has values of any kind, with any structure.
A section consists of a set of values from the stalks over an open set in the space. A sheaf has the "gluing" property,
whereby if two sections are the same over the intersection of their underlying open sets,
then there is a section over open sets that include those two open sets with values equal to those of the original two sections over shared points in the topological space.
A sheaf means that a global section (a smooth quilt) can be sewn across those sections.
Sheaves are natural models for the way the brain works.
The brain stitches together activity across open sets in time and space to form a continuous experience.
Mountcastle (1957) described the structure and function of somatosensory cortex in terms of columns,
which are like stalks over the tangential organization (that is, the surface parallel to the layers of cortex).
For the somatosensory cortex, the tangential dimensions map the body surface, that is, space.
For each point on the body, a number of different sensory submodalities can be found,
including fine touch, pain, temperature, vibration, and the state of that part of the body.
The stalks consist of values of these properties, so the range of temperatures, the frequency of vibration, and so on.
If an extended object touches our skin, individual neurons respond to the local properties,
and the brain puts that information together and creates activity that we perceive as a shape, or we recognize the object.
Similarly, if our skin is contacted by some object in some way that changes over time,
we can tell whether it is moving in a particular direction and how its properties are changing,
leading to knowledge about what is going on (e.g., a drop of water is rolling down our shoulder).
Looking back at the sort of sheaf examined above in Fig. 14, we consider the sheaves of breakfast and lunch (Figure 21).
The active stalks at these two times are about a quarter cycle apart around the period of a day.
This quarter cycle phase difference is the key arrangement for combining local information into a novel, more global property,
as will be described in detail below.
Ocular dominance is a less salient variable than orientation for most people.
Other simple variables important in V1 include contrast, color, spatial frequency (how rapidly contrast changes over space),
preferred direction, and temporal frequency (how rapidly contrast changes across time).
A visual scene can be thought of in terms of choices of these features over each open set in space,
corresponding to the activity of neurons in visual cortex.
Figure 23 attempts to illustrate this sort of sheaf. The color image is an actual representation of how orientation is mapped onto primary visual cortex.
Each color corresponds to a particular orientation, as shown at the right edge, so this is a pseudocolor map of orientation preferences across a patch of cortex.
The map is derived from an experiment where the cortex is imaged while gratings of different orientations are presented.
A patch of activated cells tends to reflect slightly less light than neighboring inactive cells, so capturing images at a series of grating orientations permits this map to be assembled.
You can see the effect of the hairy ball theorem at several places in the image, where the different colors come together.
This area was termed a pinwheel, because the various colors rotate around it.
A question arises from knowing that cortex must contain pinwheels: how do cells in the pinwheel respond to different orientations?
They could respond to all orientations, but such cells are rarely observed.
Alternatively, the pinwheel region could comprise a mixture of separate neurons that preferred different orientations from each other.
Reports have suggested that the orientation tuning of the neurons in pinwheels sharpens at low contrasts,
perhaps reflecting recruitment of longer range inputs.
Evidence has been found that single neurons in the centers of pinwheels have strong orientation selectivity,
and are segregated as in areas away from the pinwheel centers.
This example of a sheaf corresponds to a few hypercolumns, containing millions of neurons.
We are primarily interested in single neurons, and will treat a single neuron's receptive field as a sheaf.
An analogous sheaf to the hypercolumn above can be devised with the base space of time.
Just as the spatial sheaf will vary over time, the temporal sheaf varies over space.
This can lead to using a topological space uniting space and time,
but for now we'll try to simplify things by restricting our base space to just time,
as if we're only treating a single neighborhood in space with its spatial stalk.
Hubel and Wiesel
described two main types of cells in cat primary visual cortex, that they called "simple" and "complex".
Simple cells have spatially separated regions that respond to either increases or decreases in luminance (Fig. 44).
Complex cells respond to both increases and decreases in luminance throughout their receptive fields.
They theorized that complex cells were created by convergent inputs from simple cells with overlapping receptive fields.
David Hubel had a mathematics background, and saw that this operation of creating complex cells by putting together inputs from simple cells could be generalized.
He termed the abstraction of this process "complexification" (see p. 3406).
He saw this operation as appearing throughout cortex, building increasingly complex response properties in neurons with increasingly large receptive fields.
It turns out that complex cells are usually created directly from LGN inputs rather than from cortical simple cells,
but Hubel's insight that cortical processing might occur through such a general mechanism has considerable merit.
The single neuron version of the hypercolumn sheaf defined in primary visual cortex can be complexified into another sheaf by starting with two sheaves (Fig. 24).
Say that one sheaf (RF2) has a value of orientation that represents vertical over an open set in visual space, and a null value outside that open set.
The other sheaf (RF1) has an orientation just off vertical over an open set that is shifted in space relative to RF2.
Together, the two neurons responding to these orientations over slightly different portions of space could provide input to another neuron (in white)
that would thus respond to a curved contour that bends away from vertical in the lower part of its receptive field.
Hubel and Wiesel labeled such further complexified cells "hypercomplex", but they are known as "end-stopped" because they respond better to short contours than to longer contours.
When we see something, we typically note a whole set of characteristics of objects.
For instance, the shape, the color, perhaps the use, and numerous other qualities come to mind.
The classic example is seeing a yellow Toyota Prius Prime.
The question is how does the brain let us be aware of the combinations of different aspects of what we're seeing (or hearing, smelling, feeling, tasting, ...).
Such questions are known as the binding problem.
Music and speech once again present excellent examples. We assemble a gestalt perception while listening to music,
rather than separating rhythm, meter, timbre, melody, harmony, and form (although we can consciously separate them by concentrating on one aspect).
We similarly extract the semantic content of speech from the sequences of phonemes that form words,
the tonal changes that are clues to what's being expressed, and the context behind what's being said.
The issue arises in large part because different parts of the brain seem to process these different aspects.
Color is processed in cortical area V4, though also elsewhere. Inferotemporal and frontal cortex might be responsible for semantic information.
The spatial organization might depend mostly on parietal cortex. We don't understand exactly how the yellow gets together with the type of car.
Given that the number of combinations of the vast number of objects and their characteristics might exceed the capacity of the brain,
neuroscientists have proposed mechanisms to handle this issue.
As will be discussed in the next chapter, we are talking about how novel cognition emerges.
The brilliant pioneering neural modeler Christof von der Malsburg proposed, and the equally brilliant neurophysiologist Wolf Singer,
working with Charlie Gray and others, popularized the idea that binding is created by synchronous activity across populations of neurons.
For many decades, we have understood that the brain contains electrical signals from groups of neurons whose activities oscillate at different temporal frequencies.
Electroencephalographic (EEG) recordings from scalp electrodes reveal such oscillations across several frequency bands.
They were named δ: 0.5-3.5 Hz, θ: 3.5-7 Hz, α: 8-13 Hz, β, 18-25 Hz, and γ: 30-70 Hz.
Singer argued that approximately 40 Hz oscillations in the γ band occurred in visual cortex and other parts of the brain,
and that the activity in distant sets of neurons could be synchronized.
That is, oscillatory spiking patterns that occurred over fairly short durations could have their spikes within milliseconds of each other.
Note that the presumed mechanism for generating oscillations, and perhaps local synchrony, involves inhibitory neurons that set timing.
How these separated populations of neurons might achieve synchronization has not been clarified,
and experimental evidence for the binding by synchrony hypothesis is mixed.
Nevertheless, this compelling idea caught fire, and was stretched to great heights.
The ideas that the mysteries of consciousness and spiritual insights could be due to oscillations and synchrony were posited.
Nick Swindale, another brilliant and imaginative neuroscientist, came up with a fascinating mechanism for the
effects of inhalation anesthetics.
He noted that anesthetics can affect the lipid membranes of cells, including neurons.
In neurons, that can alter the conduction speeds of axons. Faster and more variable conduction might alter the ability of the brain to generate synchronized firing.
This might produce the loss of consciousness elicited by these anesthetic agents.
The grand claims might not win the day, but synchrony, with or without oscillations,
remains a key step in understanding how the brain puts together bits of information in the form of neuronal activity into more informative bits.
In the hippocampus and related structures, what are called sharp wave ripples occur.
These are short bursts (30-100 ms) of spike trains at high frequencies (140-200 Hz) across thousands of neurons.
Ripples appear to be important for memory mechanisms. They are one of many components of memory consolidation and recall.
Slower oscillations such as θ are equally important.
What we argue here is that considering just synchrony leaves out the bulk of the story.
Instead, one must look at relative timing as a whole: all phases matter, not just zero phase.
In addition to the frequency bands at which neurons oscillate spontaneously,
one must study the range of frequencies created by external inputs and motor functions.
We don't have explanations for solving the combinatorial explosion problem, or for combining activity across distinct parts of the brain.
However, we propose what is a somewhat novel way of looking at the creation of emergent properties and globalization, employing sheaf theory.
Binding is a form of stitching.
What is the emergent property in the example of Figure 24? It is the curvature, not present in either input.
This is a simplified toy example, but it qualifies as an emergent property.
Timing is not part of the example, however, and we will concentrate on timing's key role in most emergent properties.
Generally, sets of local neuronal activations, having different phases on their own,
have their phases shifted by other response properties so that they coincide and lead to activation or suppression of other neurons that convey novel response properties.
We can take one neuron, Pyramus, that responds at some phase PA when some process A is happening, and another neuron, Stella,
that responds at a different phase SA when that same process A is happening. These are the local elements.
Let's say that Pyramus responds with some phase PB when process B occurs, and Stella is active with some phase SC during process C.
If process A happens in conjunction with process B, then Pyramus will be active with a phase that is the sum of the phases for A and B.
If A and C are happening, Stella will have the sum of its phases for A and C.
The neurons will be active in phase with each other if PA+PB = SA+SC.
This simple explanation may capture much of the seemingly mysterious way that the brain creates these novel emergent properties.
The details are of course the key to understanding each instance of how this comes about.
We describe below how a fundamental example, direction selectivity, works.
In that case, process A can be a temporal change in luminance for visual neurons, and processes B and C would be different locations in space.
Pyramus might have a phase of 0 c for luminance, meaning it responds near peak luminance. Stella might have a phase of ¼ c for luminance.
But if Pyramus has a spatial receptive field with a spatial phase of ¼ c and Stella has a different location,
with a spatial phase of 0 c, then for a moving stimulus that activates the two locations at different times,
the phases of both neurons would be ¼ c and their activity would coincide.
If they both excited another neuron, that neuron would respond to the moving stimulus.
As shown below, if the stimulus moves exactly the same but in the opposite direction,
the phase values of the two neurons would be out of phase, leading to no response from the downstream neuron,
which would thereby be direction selective.
The original two neurons are not direction selective, but their convergent inputs produce this novel property.
This paradigm of direction selectivity covers a tremendous amount of ground.
Every neuronal response property varies over time, and what we want to know is the direction in which it's changing.
Our lives consist largely of doing things in one order rather than in the reverse order.
We are aware, consciously or most often not, of the directions that things in the world are changing,
and we behave in highly ordered ways, in sequences and continuously.
All of our behaviors are directed in time.
A familiar example of the mysteries of emergence and globalizing lies in face perception.
Thinking of this as a purely spatial problem, one might wonder how we put local features such as eyes together,
when each eye could appear practically anywhere in visual space, since the face can be at a wide range of distances and viewing angles.
The early visual system is retinotopic, preserving the spatial coordinates inherited from retina.
However, other parts of visual cortex lose retinotopy, and it seems more difficult to understand the spatial coordinates used for processing features like eyes.
As described above, the solution is simply to think in terms of phase.
Neurons in these non-retinotopic visual areas can respond at specific spatial phases.
In the example of a face, the eyes tend to fall at well-defined phases relative to the boundaries of the face.
Neurons sensitive to eyes and having certain relative spatial phases could converge to help generate face-specific neurons,
in analogy to the process that produces direction selectivity.
This illustrates the concept of invariance. A face is the "same" no matter where it is placed in space,
no matter the size of its projection on the retina. What counts is the relative positions of features, that is, their phase.
Analogously, we recognize what different people are saying despite their voices using different pitches.
Melodies sound similar despite being played in different keys. The relative pitches are perceived.
Buonomano has some great examples of emergent properties, and how our perceptions consist of integrations of "shards of time".
This integration is easy to understand when we realize that neuronal processing is continuous and extended in time.
The syllables "po" and "camp" in the word "hippocampus" are like Stella and Pyramus,
they are combined into the word based on their relative timing. He also gives the example of saccade compensation,
but only in terms of going blind during saccades, not recognizing that timing is also important.
We routinely run into examples of emergent properties.
Cooking is all about mixing ingredients that differ from each other to make dishes with novel flavors and textures, like Sweet and Sour sauces.
Individuals with numerous differences come together as couples. Sports put together varying tools like balls and bats.
A set of letters enables writing, and phonemes speech.
The ultimate example of emergent properties is consciousness. Although notoriously hard to define,
consciousness has something to do with thinking, a largely non-motor behavior.
Just as the motor system depends entirely on time, thinking involves sequences of ideas that are organized into orders.
These orders are generally determined by associations.
Consciousness appears to be closely related to memory.
Memory is in turn all about associating processes that are separated on the line of time, but have common phases over some periods.
Mechanistically, neurons have activity at those phases, are therefore coincident, and produce associations.
Again, this is phenomenological, and the detailed mechanisms must be demonstrated.
In physics, emergent properties abound. Superconductivity is an example. At low temperatures,
the properties of the many electrons in certain materials change microscopically
(at the quantum level: electrons bind together in "Cooper pairs")
and macroscopic behaviors of the material arise whereby the electrical resistance vanishes.
Local structures can lead to global phenomena that are at least difficult to predict.
A simpler example is water, that emerges from the elements hydrogen and oxygen.
Neither element has the properties of water that emerge from their combination.
On earth, life emerged from the primordial soup. Like consciousness, life is not easy to define.
The concept of species is a bit clearer, and we understand something about how new species emerge.
We occasionally experience transcendent emotions. Could these arise from emergent emotional properties?
Perhaps when several types of emotions are felt simultaneously, relatively novel responses are generated that we interpret as transcending our ordinary experiences.
Philosophers have discussed emergent properties with respect to concepts such as free will.
Many arguments seem to place physical or neural processes at a lower level than the emergent properties they underlie,
and that free will occupies some sort of higher level.
We find these arguments ridiculous. Whatever free will might be, it would have to be a neural process.
Robert Sapolsky, a prolific neuroscientist, wrote a lovely book about this:
Determined: A Science of Life Without Free Will.
Sapolsky gives many excellent examples of emergent properties. His main concern is that the brain doesn't depend on some higher power to read out its processing:
there is no free will.
He argues that we don't need to promote free will as something above what the brain does.
People often think that if the brain does something, it's somehow not as elevated as our supposed highest experiences.
They are caught up in the reductionist fallacy, that science always makes problems trivial.
They fail to appreciate that what the brain does should be viewed as absolutely remarkable, transcendent, and beautiful.
Sapolsky characterizes free will as an illusion. I prefer the term delusion, meaning a belief that isn't true.
We are deluded about pretty much everything, because our brains create beliefs that are not thoroughly vetted by evidence,
and are always wrong in some ways, even though they might be mostly true.
Free will, time, space, color, pitch, consciousness, the safety of motor vehicles, and the sport of curling are all delusions. Sorry, Canadian friends.
Sapolsky cites studies where brain activity indicating a choice a human subject will make precedes the time when the subject believes they made their choice.
We don't have access to the underlying reasons for our choices, but mistakenly think we do.
Delusions are endemic to us as individuals, and also as populations.
Mass delusions have been catalogued and studied.
These include familiar ones like the belief in witches that lasted many centuries.
And less-known ones like the windshield pitting delusion that seem particularly weird.
A delusion is defined as a false belief. Given that our beliefs are formed based mostly on emotions, our beliefs lead to mistakes.
Daniel Wegner has made this delusion especially clear.
He argues that we mistake the fact that our actions are preceded by our expectations of them for willfully causing those actions (see their Figure 1).
He also discusses the many times when our actions are not accompanied by will.
We wrongly infer causation from temporal proximity. This is a version of the well-known fallacy of correlation not causation.
Sapolsky writes "You can't successfully believe something different from what you believe."
You can, however, train yourself to challenge your own beliefs, just as scientists and others are trained to challenge our own beliefs,
as well as the beliefs of others.
Beliefs are not as simple as they seem. Magicians, evangelists, marketers, politicians, and many other people try mightily,
and often successfully, to make us believe things we don't really believe. We are often unsure about what we really believe.
At the same time, we are completely sure of most of our beliefs. Capgras syndrome is an excellent example of how beliefs are formed,
and evidence inconsistent with our beliefs is denied.
Somebody with the Capgras delusion denies that somebody or something with whom they have an emotional relationship is that person or thing.
They will say that somebody looks just like their mother, but is not their mother.
Ramachandran (Movie 6) argues this is due to a disconnection between inferotemporal cortex,
that provides visual recognition, and amygdala, that mediates the emotional reaction.
Our beliefs are grounded in our emotions, and are quite resistant to evidence.
We need to note, however, that one kind of evidence that free will doesn't exist is based on the experiments mentioned above,
where neural activity that drives our choices occurs earlier in time than the conscious belief that the choice has been made.
What does earlier in time mean? The underlying assumption is that the neural activity and the sense of having chosen are well localized in time.
It seems more likely that these processes are both extended in time, and overlap.
The appropriate analysis compares phase vs. temporal frequency for the two processes, not arbitrary moments in time.
Sapolsky does not rely on such experiments for his thesis about free will, however.
Sapolsky discusses chaos. The butterfly effect is a popular concept, where the fluttering of a butterfly's wings in Brazil leads eventually to a hurricane in the Caribbean.
The idea is that weather is sensitive to starting conditions, so that even a tiny perturbation in the wind can lead to much larger effects.
Unfortunately, Sapolsky oversimplifies the basis of chaos, claiming it arises from nonlinearities.
That is not a great explanation. A really clear example of how to produce chaos was described by Mitch Feigenbaum, a certified genius who pioneered many aspects of chaos theory.
Figure 25 illustrates Feigenbaum's example where xn+1 = 4λ xn(1-xn).
That is, you start with x0, compute x1 based on this rule, and keep doing that for increasing n.
The parameter λ is key here, as will be explained. The starting value x0 should be between 0 and 1.
If it starts at either 0 or 1, then all subsequent values are 0.
But if it starts anywhere else, after many iterations the values tend to approach a fixed point.
For example, if λ=0.5, and we start with x0=0.1,
the rule gives us the series 0.1, 0.18, 0.2952, 0.416114, 0.485926, 0.499604, 0.5, and then 0.5 forever (green region).
If λ=0.6, the series is 0.1, 0.216, 0.406426, 0.578985, 0.585027, 0.582649, 0.583606, 0.583224, 0.583377, 0.583316, 0.58334, 0.583331, 0.58334, 0.58333,
and then it oscillates around about 0.58333 asymptotically.
An interesting thing happens as λ increases. At λ=0.75, the series oscillates between two points, one near 0.65918 and another near 0.67398.
Then, as λ continues to increase, the series oscillates between 4 points.
For instance, at λ=0.87, the 4 points are about 0.869426, 0.395064, 0.831680, 0.487159. At λ=0.89, 8 points, at λ=0.892, 16 points,
and as λ increases by decreasing amounts, the oscillations keep increasing by a factor of 2.
The number of points in the oscillation is the period, so the period doubles as λ increases.
But these doublings occur at smaller and smaller increases in λ.
At a finite λ, around 0.8925, there have been an infinite number of period doublings, meaning the period is infinite.
That means that one can not predict what the value of xn is as n gets large.
The process is chaotic. Feigenbaum's process is termed the period doubling route to chaos.
So chaos can be achieved by a deterministic process, not just by randomness. This can be demonstrated physically,
for example with chemical reactions (BZ reaction,
with a citation of Art Winfree; and a Ken Showalter presentation).
These chemical systems demonstrate emergent properties, like many biological systems as well as the physical systems noted above.
When people claim that nonlinearities are responsible for something, like chaos, they aren't saying much.
The category of nonlinearities is simply the complement of linearities.
It includes practically everything (except linear things). Some nonlinearities do one thing, others another thing.
As seen above, the behavior of a nonlinear process depends on parameters.
When we're told something is nonlinear, we should always ask, "What kind of nonlinearity?"
It's like wanting to know where somebody lives, and being told "Not in Gaborone."
Most systems have large linear components, while also showing nonlinearities, so one should keep in mind that linear and nonlinear components are combined.
Purity is rare. Oversimplification is common.
When analyzing systems, the initial focus is often on the linear components, because they can be analyzed more fully,
and generally account for more characteristics of the system. Nonlinear components typically require more complicated analyses.
One can use the linear analyses to predict how much of the behavior of the system is in fact linear,
and one gains considerable insight this way.
Sapolsky describes how the brain works in his Chapter 13 in terms of combining differing inputs to generalize across their similarities.
For instance, he puts together Gandhi, King, and the Mirabal sisters to create the concept of dying for one's beliefs.
This is probably one of the ways the brain works. But more important might be the structure outlined here,
where inputs that differ are combined to create new properties, most importantly direction.
The brain tends to signal errors. Decisions consist largely of trying to avoid errors. For instance, when we're walking around inside a house,
our brain is making lots of decisions about how to move in order to not walk into walls.
A way this works might be illuminating. Many of the pathways carrying information about motor plans pass through the cerebellar nuclei (Fig. 26).
The motor plans are relayed to the places where the plans are carried out. But they are also sent into cerebellar cortex to be processed.
The processing there can be characterized as looking for errors.
When all looks good, the inhibitory output of cerebellar cortex (Purkinje cell activity) decreases,
permitting the cerebellar nucleus cells to go ahead and relay the plans.
If something seems wrong, Purkinje cell activity increases, inhibiting their targets in the cerebellar nuclei,
stopping the motor plans from being executed at that time.
A concrete example might be that when playing the piano, if a finger is about to hit a key but the cerebellum detects that doing so would be inappropriate,
the movement is stopped.
In Sapolsky's context of making moral decisions, the brain has set up values,
and when a decision is about to be made that goes against those values, the error is detected and the decision is suppressed.
We need to question our beliefs. An extreme example is when we are emotionally affected enough to do something terrible,
like killing somebody out of anger.
We promote critical thinking, but need to teach it in that sort of context, learning to not trust our emotions and beliefs,
but instead challenge them.
Note that most of these examples of brain processing are unconscious.
The cerebellum and thalamus do not appear to participate in consciousness, though we don't understand how consciousness arises, so they might.
But the way the brain uses time is dominated by the way single neurons process time.
The sketch provided above will now be fleshed out, in a long chapter full of hard science that I've attempted to keep accessible.
But it's going to be a rough bit of reading, I suspect.
We will cover the example of visual cortical direction selectivity in great detail.
The description of direction selectivity is like a recipe: what are the ingredients, and how are they combined?
We introduce this subject with some historical background. Many people regard the visual system in terms of camera metaphors.
Some people imagine that we see motion the way a movie camera does, by stringing together a sequence of still images.
This goes back at least as far as Parmenides' acolyte Zeno, who argued that motion can't exist because at any point in an object's motion it is not moving.
It is important to internalize how wrong this is (as noted above with regard to period doubling, adding an infinite number of small numbers can result in a finite sum).
Our perception of motion is smooth and continuous. Neurons are directly activated by light and dark contrasts that change in time.
The receptive fields of these neurons are extended in both space and time, and moving stimuli evoke spiking responses from them that vary continuously in time.
Neurons do not take pictures of the world as it changes, but instead change their firing smoothly in response to those changes in the world.
Visual cortical direction selectivity was discovered by Hubel & Wiesel (1959; see their Figure 8),
who noted that many neurons responded to stimuli moving in one direction but not in the opposite direction.
They were aware of previous work that had demonstrated direction selectivity in the retina12.
However, direction selective retinal cells do not project to cortex (they project instead to areas at the base of the brain that are important for letting us move about the world, as described below).
Other retinal cells that are not direction selective project to the previously mentioned dorsal lateral geniculate nucleus (LGN),
and LGN cells project to primary visual cortex (V1).
LGN cells are not very direction selective in some species, including primates, so direction selectivity largely emerges in cortex.
It turns out that the majority of visual cortical cells are direction selective,
and this property emerges in cells that receive direct input from the LGN (as opposed to requiring a lot of processing in cortex).
Theoretical efforts put forward various schemes by which direction selectivity could be generated.
The focus of many of these was on the role of inhibition, because blocking inhibition reduces or eliminates direction selectivity (Tsumoto et al. 1979).
Unfortunately, the usual hypothesis involved positing strong inhibition for stimuli moving in the nonpreferred direction and weaker inhibition in the preferred direction.
Experimentally, this bias was not observed (Creutzfeldt et al., 1974).
Reichardt and Hassenstein had described how direction selectivity comes about in the invertebrate eye,
arguing that the key is a multiplication of inputs that differ in space and time.
Barlow and Levick
had also demonstrated that direction selectivity in the rabbit retina depends on spatial and temporal differences that are combined in a multiplicative fashion (an "AND" gate).
The need to have the spatial and temporal differences should be obvious, since that is the basis of motion, a change over both space and time.
These are the ingredients that are used to make direction selectivity.
However, Hubel and Wiesel argued that visual cortical direction selectivity arose from interactions between ON and OFF responses13.
ON cells in retina and LGN are excited by increases in luminance, and OFF cells are excited by decreases in luminance.
In cortex, cells they referred to as "simple" had neighboring ON and OFF regions,
presumably driven by LGN ON and OFF inputs with differing spatial receptive fields (Fig. 44).
Hubel and Wiesel's idea was that as a bright stimulus left an OFF region of a cortical simple cell's receptive field,
there was a rebound excitation (the decrease in luminance).
As the stimulus entered the ON region, excitation was evoked by the increase in luminance,
and these two processes combined to generate strong excitation.
For the reverse direction, as the stimulus exited the ON region and entered the OFF region, there would only be suppression.
Many people pointed out a potential flaw in this theory, that a dark bar would have the opposite direction preference,
evoking more excitation when moving from the ON zone into the OFF zone.
Experimentally, neurons prefer the same direction for both bright and dark bars. Hubel and Wiesel almost had it right,
but they did not make it clear that timing was involved.
The field was dominated by the dichotomy between ON and OFF, and despite a partial awareness that timing was more continuous,
with sustained and transient responses, the view of time as points on a line made it difficult for people to realize that timing varied around a circle, as phase values.
In 1985, three papers were published together in Journal of the Optical Society of America (JOSA) that addressed the origins of direction selectivity.
These papers derived from psychophysical and modeling work, though they were informed by physiology.
The differences between the three contributions lay largely in the way that the ingredients might be combined:
multiplication (van Santen and Sperling),
addition/squaring/addition ("Energy", Adelson and Bergen),
or addition (Watson and Ahumada).
These papers all pointed to the need for inputs that differed in space and time.
The formal characterization of these differences, the ingredients, is known as spatiotemporal quadrature.
This just means that the spatial and temporal differences should each be a quarter cycle. Phase was recognized as the way to think about this.
We'll take an important digression here to explain exactly what this implies and why it's important.
The following paragraphs and Movie 7 are essential to understanding the rest of this book!
First, as mentioned above, motion consists of changes in space and time.
More generally, changes in other properties and time occur and might be understood in analogy to motion in space and time.
Second, the key aspect of motion is its direction; speed is secondary. Third, we need at least two inputs that differ in space and time.
More inputs can be used, but let's reduce the problem to just two for simplicity.
The diagram on the left of Movie 7 shows the two inputs that differ in space by having their receptive fields offset in space,
so they are excited by stimuli in different parts of space.
That part, the spatial difference, is easy for the brain to acquire. We know that throughout the early visual system,
starting in the retina, cells differ as to where in visual space they respond.
The temporal difference needed between these inputs is not quite as apparent,
but for now let's just say that one of the inputs has a temporal delay.
Call the spatial difference between the inputs Δx and the temporal difference Δt.
For the opposite direction, the right-hand input is stimulated first, and does excite the direction selective cell. The stimulus only arrives on the left later,
and the delay adds more time before the inhibition is passed to the direction selective cell, too late to affect it.
Hopefully this is simple to understand. This is all that is involved, in a sense. In one direction, the inputs arrive onto the direction selective cell at the same time (and in this way of combining the inputs, the inhibition blocks the excitation).
In the other direction, the inputs arrive at different times (so the inhibition is ineffective).
The key to this model is that the difference in direction of motion is turned into a difference in timing: in one direction we get the SAME time, in the other direction DIFFERENT times.
There are complications in this scheme, arising from the fact that we're working in the time domain. The inputs arrive at the same time only if Δx/v -Δt = 0 where v is the stimulus speed.
The delay Δt between the inputs has to match how long it takes for the stimulus to travel between the inputs (Δx/v), so the speed v has to be Δx/Δt.
For the rightward direction, the time difference between the inputs is Δx/v+Δt.
If the stimulus moves too fast from left to right, it will get to the right-hand input before the inhibition arrives, and thereby excite the downstream cell.
If it moves too slowly, the inhibition will have died off before it gets to the right-hand input, and the excitation will similarly get through.
This is a real problem, that this model only works for a limited range of speeds around Δx/Δt. However, the problem is easily solved, by working in the frequency domain.
The diagram on the right is exactly the same model, but uses a different language. Instead of the spatial and temporal differences Δx and Δt, we now label them ψ and 𝜑.
These are spatial and temporal phase differences. Just by changing our language, we gain a lot. The model works exactly the same as above,
but now we can say exactly what it means for the signals to arrive at the same or at different times.
In one direction, we subtract the spatial and temporal differences, and in the other direction we add them.
For the rightward direction, we subtract them, as above, and want the difference to be zero.
For the leftward direction, we add them, and want the difference to be non-zero.
Using the language of phase, no difference is 0 c, in phase, and a maximally different phase is ½ c, out of phase.
So we can now specify exactly what we want. In one direction the difference of the spatial and temporal phases is 0 c, and in the opposite direction their sum is ½ c:
We emphasize that the key here is to turn the difference in direction into a difference in timing. We would generalize that to most aspects of brain function, where differences in function result from differences in timing.
As they say, timing is everything!
With this description in terms of phase, the model now works at any speed. That trick comes about because we insist on having the quarter cycle phase differences no matter what the stimulus might be.
In reality, if the stimulus can vary, we might have a hard time creating those phase differences across all of the stimulus variations.
Watson and Ahumada (1985) proposed this model as an ideal motion detector.
We will discuss this issue of how real neurons deviate from quadrature as the stimulus changes, but first note that real neurons do not need to be ideal motion detectors.
They do not have to satisfy the equations above exactly, but instead just need to have somewhat different responses in the two directions.
They may not achieve a response of 0 in the non-preferred direction, nor attain the maximal possible response in the preferred direction.
If the phase difference in the non-preferred direction is 0.05 c and in the preferred direction it is 0.45 c (e.g., spatial and temporal phase differences of 0.25 c and 0.2 c), the response difference would still be significant.
This is what is observed in many neurons. What is important is not so much quadrature, but that there are spatial and temporal differences.
Those differences can not approach 0 c or 0.5 c, but must be somewhat near quarter cycles. We need approximate spatiotemporal quadrature.
Phase is only part of the description of functions in the frequency domain. Amplitude also plays a role. Implicit in spatiotemporal quadrature is that the amplitudes of the two inputs are the same.
Otherwise, even though the phases subtract to 0 c and add to 0.5, subtraction and addition of the complex numbers comprising amplitude as well as phase would not lead to a maximal response in one direction and no response in the other direction.
However, this requirement to have the same amplitudes applies only to the ideal. In real neurons, the amplitudes of the inputs can be somewhat different. The way the inputs are combined plays an additional role.
For instance, a weak inhibition might be able to veto a strong excitation. In addition, we need to keep in mind that neurons are not completely linear, and they receive many inputs, not just two.
The situation quickly gets more complicated than the ideal model, which we think of as giving us ideas about what to measure: theoretically-derived heuristics.
Before getting to more technical matters, another simple way to understand the importance of quarter cycles is to ask how one would move around a clock to go from 12 to 6. You can go either clockwise or counter-clockwise equally well.
In order to specify which direction to take, one needs to add something between the half-cycle, saying to go from 12 to 6 through 3. Then it is clear that one should go clockwise.
This is what quadrature buys, a phase difference that is between zero and a half-cycle is needed to specify direction. Winter to summer can go either forward or backward in time, but adding spring tells you to go forward.
All that is really needed is some relatively small phase change, say from Monday to Tuesday for the period of a week. Note that as the change approaches either zero or a half-cycle, however, the directionality becomes less compelling.
What really counts for direction selectivity is how temporal phase varies across space. If phase just jumps by a half-cycle (i.e., from 12 to 6), one can go in either direction.
Ideally, temporal phase varies continuously and monotonically across spatial phase. If it forms a nice ramp for stimuli to roll down, you get an ideal motion mechanism with constant slope (Movie 8).
When working in the space-time domain, phenomena can be observed that seem counter-intuitive. The best-known example is called reverse-phi. Phi motion is apparent motion, created by a series of flashed stimuli at different locations, as in the signs mentioned above.
If you see a flash toward the right followed in time by a flash toward the left, you perceive leftward motion. However, if a bright stimulus is flashed on the right, followed by a dark stimulus on the left,
you can perceive rightward motion even though the flash on the right preceded the flash on the left in time. Hopefully you have already considered this stimulus in terms of phase.
By reversing the contrast of the flash from bright to dark, one imposes a half-cycle shift in phase (Movie 9). So now instead of the stimulus moving from 12 to 3, it seems to move from 12 to 9, that is in the opposite direction.
The quarter cycle shift in space has the half cycle added to it, giving ¾ cycles, which is equivalent to -¼ cycles.
Our examples from the visual system certainly do not mean these emergent properties aren't ubiquitous. The most important of our sensory systems, vestibular signaling, is completely directional.
The vestibular system relays information about how our heads are moving in space and time: left-right, up-down, forward-backward, and rotating on the axes of our necks, shaking either yes or no.
Much of the input to the brain from the vestibular system targets processes that are unconscious. An important example, to go back to the visual system, is the vestibulo-ocular reflex.
When our heads move, our eyes, which are stuck in our heads, move as well. This can throw off our ability to tell what we're looking at. So the brain uses the vestibular signals about how our heads are moving to compensate for the head motion with eye movements.
This allows us to see clearly when we're walking, for instance.
We feel motion across our skin with direction selective cells. We appreciate changes over time in taste and smell in terms of their directions. For hearing, the analogue of visual or skin space is the tonal frequency.
We hear rising and falling tones with direction selective cells, letting us decipher speech, enjoy music, recognize bird calls, and a myriad of other auditory behaviors.
But the place where direction is probably most needed is in the motor system. Our movements are almost always directed in time.
We move our hand to grasp a pen and write with it in a series of directed steps.
Our brains program our movements based on the desired task, then release the motor neurons that drive the muscle fibers to contract and relax according to plan.
Each muscle fiber moves a little part of the body in a certain direction when it contracts or relaxes.
The superior colliculus is a pair of hills in the midbrain of mammals, comparable to the tectum in other vertebrates.
It is a site of orienting behaviors, creating movements in space and time related to sensory stimuli.
If you hear a sound to your right, you might turn in that direction. In the superior colliculus, eye movements are programmed. The direction of an eye movement is derived from the anatomic location of activity across the superior colliclulus.
At one end of the colliculus (the rostral end), activity produces short saccades. At the other end, longer saccades are generated by activity spread over much of the colliculus that reaches the caudal end.
The left hill moves the eyes to the right, and vise versa. The medial and lateral sides move the eyes up or down.
Collicular function provides a prime example of how population activity can be used, as opposed to neuronal specificity.
Activity at the rostral pole of the colliculus not only corresponds to short eye movements, but actually holds the eye in place, enabling us to fixate on what we want to see.
As noted above, even while fixating, our eyes do move, including making very short saccades. Blocking activity in the rostral neurons decreases the rate of microsaccades (Hafed et al. 2009).
The direction and magnitude of the microsaccades still corresponds to the location of activated neurons.
Morrone extended her work described above in several ways, including how motor activity influences timing, and how direction is involved.
Other studies have suggested how timing varies across the nervous system and muscles during movements (Breteler et al. 2007; Hatsopoulos et al 1998).
Zagha et al 2022 discussed how movements in awake mice produce activation across the brain that is stronger than sensory or cognitive signals.
Less transparent than for movement is how our emotions and moods are directed in time. Our experience is that these certainly do change, and we know in which direction our feelings are going.
These changes are slower than most of what our sensory and motor systems experience.
Other slow processes, like going to school for many years or working on a long project are clearly directed in time, and we know whether we're near the beginning, middle, or end.
That is, we are aware of what phase we're in.
Everything the brain does, it does over time. Its activity changes over time in a highly directed manner, relying on neurons that fire differently for the different directions of whatever processes those neurons are involved in.
We now turn to the story of how the brain implements this model. In the 1980s, David Mastronarde noticed that some of the LGN cells he recorded had unusual responses of a kind not previously published. These were the lagged cells illustrated above.
Since the 1960s, it was known that many cells in the LGN and other thalamic nuclei participated in a triadic synaptic arrangement.
The LGN triad consists of (1) the excitatory synapse of the retinal ganglion cell axon onto a dendrite of a geniculate relay cell (relay cells project to cortex; these cells include all lagged cells as well as many nonlagged cells);
(2) an excitatory synapse from the retinal axon onto a dendrite of an inhibitory interneuron (the other kind of LGN cell, interneurons do not project to cortex; interneurons are all nonlagged);
and (3) an inhibitory synapse from the interneuron's dendrite onto the relay cell dendrite. Fig. 27 shows this schematically with some additional details: the postsynaptic receptors mediating the synaptic responses vary, and the whole structure is wrapped in a glial sheath.
Mastronarde provided a vast amount of data detailing the origins of lagged cell responses and contrasting them with nonlagged cells (Mastronarde 1987a, Mastronarde 1987b).
First, he confirmed that all lagged and most nonlagged cells receive a single dominant input from one retinal ganglion cell.
He noted that he only recorded lagged cells with certain electrodes, and that the parameter that best distinguished lagged and nonlagged cells was their "antidromic latency" from cortex.
Antidromic latency is how long it takes for a spike generated in cortex (by experimentally providing electrical stimulation there) to travel to LGN, in the reverse direction along the axon.
Lagged cells often had extraordinarily long antidromic latencies. The inference is that their axons have small diameters, which slows the conduction speed of spikes. Neurons with fine axons have small cell bodies.
The difficulty in recording lagged cells with many electrodes arises because of these small cell bodies, since most electrodes will only "hear" large cells that swamp the many smaller cells in their vicinity,
like listening to a crowd where a few people are shouting and most are whispering. An electrode needs to get very close to a small cell to hear it, putting its ear up to the cell's mouth, to extend the analogy.
Hubel and Wiesel recognized this problem, though they didn't try to solve it:
"Other types of receptive fields may yet be found in the cortex, since the sampling (45 units) was small, and may well be biased by the micro-electrode techniques.
We may, for example, have failed to record from smaller cells, or from units which, lacking a maintained activity, would tend not to be detected.
We have therefore emphasized the common features and the variety of receptive fields, but have not attempted to classify them into separate groups."
Confirmation of many of Mastronarde's results was obtained (Humphrey and Weller, 1988a),
and extended by filling neurons intracellularly with the dye horseradish peroxidase (HRP) after recording their visual responses (Humphrey and Weller, 1988b).
The HRP provides a way to visualize the structure of the neuron after sacrificing the animal, fixing the brain tissue with aldehydes, and cutting and preparing sections of the LGN to be viewed under a microscope.
They demonstrated that all lagged cells have small cell bodies and fine axons. They also showed that lagged cells have a particular morphology, showing dendritic appendages known as grape clusters (Fig. 28).
These appendages are the sites of triadic synapses. Some LGN relay neurons have many appendages, others have fewer, and some have none. Nonlagged cells can have dendritic appendages or not, and typically have larger cell bodies than lagged cells.
The triadic synapses transform the retinal input. The inhibition inverts the sign of the input, providing a half-cycle shift in phase.
Then, the excitatory transmission through the NMDA receptors creates firing in the lagged cell when the inhibition declines. This response to the change in inhibitory input provides a quarter-cycle shift.
That is, the response does not occur when the retinal cell is simply not firing (as would be the case for a half-cycle shift), but when the retinal cell's firing changes by having its rate go down (this is like the negative of the derivative, producing a quarter cycle phase lag).
For the step stimulus, the retinal cell gives a transient rise in firing at onset, and therefore a strong inhibition in the lagged cell (Fig. 6; figures 3 and 8 in Saul 2008).
As that retinal transient goes away, the lagged cell starts firing. The retinal cell then continues to decline in firing rate during the step, so that the lagged cell continues to fire.
At stimulus offset, the retinal cell suddenly stops firing and the inhibition ends while the NMDA-mediated excitation persists, leading to the strong anomalous offset discharge in the lagged cell.
The inversion and differentiation combine to produce a quarter cycle phase lag between the retinal input and lagged cell output. Nonlagged cells relay their retinal input with relatively little change, though both lagged and nonlagged cells vary widely.16
Lagged cells can be difficult to record, because they don't fire immediately when the stimulus changes, and many of them do not fire at high rates.
One needs to be patient and gentle with them. Whereas most visual neurons announce themselves loudly,
lagged cells sometimes only reveal themselves with murmurs. After recording from many lagged cells,
one learns what they sound like (the electrical signal recorded from neurons is fed to a loudspeaker, and spikes are heard as sharp pops, as in Movies 2 and 3).
The first lagged cell recorded in an alert monkey was being tested by Elsie Spingath and Yamei Tang, who had never heard a lagged cell.
I was sitting in the lab and got tremendously excited by hearing the familiar tune. We wound up testing that cell extensively
(just three of the dozens of tests that were run were illustrated in figures 2, 3, and 4 in Saul 2008), until we had to leave for a seminar.
Once you peel back the curtain on them, they can provide hours of fun as you test them with various stimuli.
They are a bit like babies who can't talk much but nevertheless have a lot to say.
Lagged and nonlagged cell responses are separated by about a quarter cycle in time because of these mechanisms. Recall, however, that phase is just one dimension of time, the other being temporal frequency (or its reciprocal, period).
At what temporal frequencies are lagged and nonlagged cells in quadrature? One might hope that they would remain a quarter cycle apart across all frequencies, as in the ideal motion detector.
Keep in mind that low temporal frequencies are particularly interesting, for one because most of our behavior takes place over long periods/low frequencies. Can a lagged cell provide a quarter cycle phase lag over many seconds?
If the input firing changes very slowly in time, will the triadic inhibition be competent to delay output firing for many seconds?
We performed simple experiments in cats to measure timing in lagged and nonlagged LGN cells. The small spot used for the step stimulus had its luminance modulated sinusoidally in time at a series of temporal frequencies (Movie 3),
and we measured the phase of the response relative to the stimulus. Figure 29 shows responses to a spot modulated at 1 Hz for an OFF-center nonlagged cell, an ON-center lagged cell, and an ON-center nonlagged cell.
The nonlagged cells fire a half-cycle apart, as luminance is either falling or rising. The lagged cell fires halfway between the two nonlagged cells, and thus can be seen to be about a quarter cycle away from either of the nonlagged cells.
To be quantitative, we measure the phase relative to the stimulus luminance peak. The OFF-center nonlagged cell has a phase value just less than 0.5 c; the ON-center nonlagged cell is just less than 0 c; and the lagged cell is just less than 0.25 c.
Figure 30 illustrates what happens at 10 frequencies, from 0.25 to 16 Hz. With increasing frequency, you can see that the responses occur later in the stimulus cycle. Again, this is due to latency.
To repeat the explanation given above in the context of this concrete example, if it takes 100 ms for a cell to respond to a stimulus, then, at low frequencies/long periods, that delay is a relatively small part of the stimulus cycle.
At 1 Hz, 100 ms is 0.1 c. But as frequency increases and period decreases, the fixed latency is an increasingly large portion of the cycle. At 4 Hz, 100 ms is 0.4 c.
Both the lagged and nonlagged cell show this increase in phase with frequency, but the lagged cell is clearly getting later at a faster rate. The quarter cycle difference at 1 Hz increases to about a half cycle by 4 Hz.
The lagged cell has a longer latency than the nonlagged cell.
The response phase values over a series of frequencies are plotted against frequency for these two cells (Fig. 30c). The points for each cell fall approximately on a line.
The best fit lines are parametrized by a slope (latency) and an intercept (absolute phase). The lagged cell has a longer latency, and an absolute phase lag relative to the nonlagged cell.
The difference in latencies is about 60 ms (0.06 s). Therefore, between 0 and 4 Hz, the phase difference increases by about 0.24 c (0.06 s x 4 c/s).
The quarter cycle difference at low frequencies increases to about a half cycle at 4 Hz.
Because quadrature is not maintained across temporal frequencies (figures 30 and 31), combinations of lagged and nonlagged cells might be expected to lead to direction selectivity at low, but not at higher frequencies.
The brain might find a way around this, for example by picking out cells with more similar latencies,
so that the phase difference at low frequencies is maintained over a wider range of frequencies (end of Saul & Humphrey 1990).
My feeling upon first thinking about these data was that cortical neurons managed some such trick, based on experience-dependent selection of inputs that would lead to direction selective responses independent of frequency.
However, we proceeded to record from visual cortical neurons, and one of the experiments we did was again very simple. We recorded responses to drifting gratings moving in each direction at a range of temporal frequencies.
To my surprise, many cells responded like the example in Fig. 32.
These cells were direction selective at low frequencies, but lost their direction selectivity around 4 Hz and above.
After awhile, it became easier to recognize these fairly common cells.
A well-known film made by Hubel & Wiesel showing them plotting a direction selective cell (6 minutes in) illustrates this kind of response,
direction selective for slow but not faster stimuli.
Note that these findings depend heavily on analyses in terms of phase. It would be difficult to understand the temporal frequency tuning of direction selectivity and its basis in timing differences without relying on phase measurements.
The fact that latency is the slope of phase vs. frequency showed us that lagged and nonlagged cells are in quadrature at low but not higher frequencies. Since direction selectivity is related to quadrature phase, we could have predicted what we later were surprised to find.
A key observation that arose from these findings is that temporal quadrature is difficult to obtain at low temporal frequencies. Figure 34 illustrates the relationship between frequency and time delays that provide quadrature.
At low temporal frequencies, long time delays are required, and they vary over a wide range of delays for a narrow range of frequencies. From 1 Hz down to 0.25 Hz, the delays go from 250 ms to 1000 ms.
It is therefore hard to imagine obtaining quadrature at low frequencies from mechanisms that operate in the time domain.
The result discussed above, what I call the temporal frequency tuning of direction selectivity, is hypothesized to arise from the temporal frequency tuning of the phase differences in the geniculate inputs to visual cortex.
The similarity of these two sets of tunings in adult cat provides some evidence, and we eventually found more evidence by examining two other cases of geniculocortical projections.
Several other findings supported this hypothesis.
Comparing the geniculate and cortical distributions of latency and absolute phase in Fig. 31 shows their similarities.
Jack Pettigrew taught me that Developmental and Comparative Neuroscience are necessary components of this research. I followed his advice in this case. First, we looked at the development of timing and direction selectivity in kittens.
Hubel & Wiesel had observed that direction selectivity was present in the visual cortex of kittens even before they opened their eyes at about 3 weeks of age, that is, without visual experience.
We measured responses from LGN and V1 neurons in kittens from 4 to 12 weeks old (Saul & Feidler 2002). In young kittens, most LGN cells had sustained responses, with absolute phase values near 0 c. These cells had, on average,
longer latencies than in adults, with a wide variance in those latencies.
What that means for the temporal frequency tuning of phase differences is that, at low frequencies, phase differences are small, since most cells are fairly sustained. However, the large degree of variation in latencies means that, at higher frequencies,
phase varies substantially between many cells. The prediction is that direction selectivity in cortex would be tuned to higher frequencies. This is what we found. Many cortical cells in young kittens were direction selective, but mostly at 2-4 Hz and not as often at 1 Hz.
Hubel and Wiesel did not measure how direction selectivity was tuned. Figure 33 shows this difference between the temporal frequency tuning of direction selectivity in kitten and adult cortex.
By the way, the reason for the timing properties in kittens probably lies in a late development of inhibitory mechanisms. Inhibition creates both transient and lagged responses, late and early inhibition respectively.
It appears from our study and others that inhibition matures quite late. Timing in kittens remains immature even after 8 weeks, when many other properties appear adult-like. In humans, I have often remarked at the poor timing I see in adolescents,
particularly on the soccer pitch. Otherwise talented players have difficulty intercepting a rolled ball.
We then examined these issues in monkeys for a comparative experiment. Timing varied at low frequencies, with transient, sustained, and lagged responses.
Latencies, however, were relatively uniform compared to cat, with few responses having the long latencies that are common in cat (Figure 5 in Saul 2008b).
The prediction from this is that direction selectivity should be present at low frequencies, and it should persist across higher frequencies, rather than go away as in cat.
Again, measuring responses to gratings drifting at different frequencies in both directions in cortical cells validated this prediction. In monkeys, cells tend to be direction selective across a wider range of frequencies (Figure 35).
A series of further experiments (Saul & Feidler 2002; Humphrey et al. 1998 - strobe rearing; Lagged review;
Monkey lagged cells) were consistent with the hypothesis that the diversity of timing in LGN provides visual cortex with the basis for direction selectivity.
The temporal frequency tuning of direction selectivity in cortex matched what was seen in LGN (Figure 11 in Saul et al 2005).
12 The mechanisms that produce retinal direction selectivity are fascinating.↩
13 "In many units (Fig. 7) the responses to movement in opposite directions were strikingly different.
Occasionally when the optimum direction of movement was established, there was no response to movement in the opposite direction (Fig. 8).
Similar effects have been observed with horizontally moving spots in the unanaesthetized animal (Hubel, 1959).
It was not always possible to find a simple explanation for this, but at times the asymmetry of strength of flanking areas was consistent with the directional specificity of responses to movement.
Thus in the unit of Fig. 7 best movement responses were found by moving a slit from the inhibitory to the stronger of the two excitatory regions.
Here it is possible to interpret movement responses in terms of synergism between excitatory and inhibitory areas.
This is further demonstrated in Fig. 10B, where areas antagonistic when tested with stationary spots (Fig. 10A) could be shown to be synergistic with moving stimuli,
and a strong response was evoked when a spot moved from an 'off' to an 'on' area."
↩
14 The identification of these receptors is due to Paul Heggelund and Espen Hartveit.↩
15 Mastronarde called X-cells that were lagged XL and nonlagged X-cells XS (single input). We refer to nonnlagged X-cells as XN. There are also lagged and nonlagged Y-cells.↩
16 Much of the variability of the geniculate neurons arises from the variation in their retinal inputs. How transient and sustained lagged and nonlagged geniculate neurons are depends on how transient and sustained their inputs are.↩
17 Note that the longer latencies in cortex are not due to conduction delays, which are less than 10 ms. The latencies are primarily accounted for by the integrative processes neurons perform, putting together inputs to multiple synaptic sites.↩
It might help to play a bit at this point. Let's explore some stimuli that are sorts of illusions.
An alternative stimulus consists of random dots, some of which move toward the left and others just appear and disappear randomly (Movie 12). In this case, the visual system has a difficult time tracking any features.
Nonetheless, a clear direction of motion is perceived.
Bill Newsome and associates used these random dot stimuli to demonstrate a connection between neuronal activity and behavior. Such a connection is termed a "linking hypothesis", and has been a challenge to demonstrate.
In Newsome's experiments, macaques were trained to report the direction of motion in these random dot displays by making an eye movement in the perceived direction.
Simultaneously, recordings were made from single cells in visual cortical area MT, where almost all of the cells are direction selective.
When the percentage of dots moving randomly was low, so that the motion was highly coherent, the monkeys responded correctly on almost all trials, and the neuron's response was strong when the dots moved in the preferred direction and weak in the nonpreferred direction.
When the dot coherence was lower, the monkey's decisions and the neuron's firing became less reliable. They computed psychometric functions describing the monkey's behavior and neurometric functions for the neuron's firing, and showed that they were closely related.
They estimated that the monkey's decisions could be determined based on the activity of about 20 neurons.
These moving dot stimuli are useful for adaptation experiments (see below) as well, at least when one isn't concerned so much about frequency specificity. Such adaptation experiments don't seem to have been applied to experiments like Newsome's, however.
Numerous other stimuli are used to understand vision. One of the great things about studying vision is that we can produce so many stimuli to probe the system. We primates are highly visual animals, and have enormous visual abilities.
Movie 12 presents several of the stimuli that we used to obtain data. A series of bars are shown at different positions across the receptive field. Each bar's luminance is modulated over time. These 6 examples employ a variety of modulation patterns.
These include binary white noise; Gaussian white noise; naturally modulated noise; sinusoidal modulation at different frequencies; spatially correlated natural noise; and sparse noise.
The term "white" here means uncorrelated, whereas "natural" implies correlations over time exist.
Sound 1: Shepard tone
The tritone paradox is made from a pair of Shepard tones that are a tritone (half an octave, or a flatted fifth) apart. They are the analogue of going from 12 to 6, or 1 to 7, etc., on the clock.
Again, jumping a half cycle does not give a clear sense of direction.
Sound 2: Shepard Tritone
Deutsch' tritone paradox is that some listeners hear the tritone change as moving up and others as moving down, and one listener will hear one change as up and another as down.
See for more discussion.
Sound 3: Tritone paradox
Music and language are wonderful places to study time. Although also true for vision, it seems to be clearer to most people that hearing depends deeply on timing.
In most music performances, structures are created at a series of time scales. The form is revealed over relatively long periods, there might be a repeated chorus of 32 measures, during which repeated 8 bar sections occur, and each bar has a structure of notes related to beats.
Musicians play with these temporal structures, varying the phases at which substructures occur.
Similarly, spoken language unfolds over time, based on semantics, syntax, phonology, tone, and numerous other ways of varying what we say. Languages differ greatly in the timings of their spoken discourses.
Tallal's work on children who have trouble in primary school demonstrated that the affected children don't process the rapid tonal changes that make up the phonemes for certain consonants.
The sounds of 'ba' and 'da' differ only during a period of about 40 ms, where 'da' has a descending frequency component (Figure 36). The affected children can't hear this difference, and so when told "This is a 'b', and this is a 'd'", they can't make the association.
Because those ba and da sounds are also associated with other sounds, bar and dark are not processed correctly, and the phrases and sentences and paragraphs and discourse that contain them can be misunderstood.
These children can learn to compensate, however.
Vestibular sensations occur over a range of time scales. One of the many important roles for this modality is the vestibulo-ocular reflex (VOR). The direction of gaze can be centered on an object of interest despite head movements, for instance while walking.
The VOR compensates for head movements at high frequencies (0.5 to 2 Hz), and the optokinetic reflex handles lower frequencies (0.05 to 0.5 Hz).
The illustration in Figure 37 demonstrates the McCollough effect. If you spend a minute or two looking at the white circles in the upper colored gratings, followed by looking at the black and white gratings at the bottom,
you should see faint tinges of color, with the vertical gratings having a reddish tint and the horizontal gratings a greenish tint.
A simple color aftereffect, where exposure to green leads to red afterimages, and vise versa, is combined here with orientation specificity.
Notably, the effect can be extremely long-lasting. Adapting to the colored vertical and horizontal gratings for 15 minutes will allow the color on the black and white gratings to still appear weeks later.
This suggests that afterimages, which are due to retinal changes, do not explain the effect, but instead some form of learning might be involved.
Adaptation has been an important technique for studying how humans sense the world. It can also be applied to the neurons that underlie our sensations.
Stimulating a visual neuron with a drifting grating makes the neuron less responsive to subsequent stimulation at the frequencies of the adapting grating.
The specificity of adapting single neurons in both the spatial and temporal domains was investigated by Saul and Cynader.
In the process of gathering these data, we observed another effect but did not report it in those papers.
Simple cells respond to drifting gratings with firing during half of the cycle over which the grating moves across the receptive field. If the grating is drifting at 1 Hz (so one cycle lasts for 1 second), there will be activity over about a half second,
then little activity over a half second, and this pattern will repeat over subsequent cycles of the drifting grating.
We adapted simple cells with a high-contrast drifting grating for 8 seconds, followed by testing with a lower contrast drifting grating for 4 seconds.
On interleaved control trials, during the initial 8 seconds there was no grating, with the same test stimulus during the final 4 seconds.
Comparing the responses to the test stimulus between the adapted and control conditions, we saw that response amplitudes were decreased by adapting.
But we also noticed that timing was affected in a very specific manner by adapting.
Figure 38 shows an example. Here, the grating drifted at 4 Hz, so one cycle lasted 0.25 seconds.
When the test stimulus was preceded by 8 seconds of no grating, the response started before the 0.125 s time point, rapidly reaching its peak above 100 impulses (spikes) per second (ips) before falling back to 0 before the end of the cycle.
The same stimulus presented after adapting evoked weaker responses, peaking at about 60 ips.
But what is most remarkable here is that the adapted response is reduced at the onset of the control response, but then catches up and is similar during the later part of the responses.
The fact that timing is not just shifted symmetrically, where both onsets and offset would be shifted, raises key questions about the mechanisms behind timing aftereffects.
Our explanation of what might be going on is presented in Figure 39. Consider two cells (for simplicity) that inhibit each other. These two cells fire a half cycle apart to a drifting grating.
When cell A is firing, cell B is inhibited, and vise versa. This is commonly referred to as "push-pull inhibition". The continuous curves show the inhibition onto each cell from the other.
We then make an assumption that adapting strengthens ("potentiates") inhibition. In the adapted state, the inhibition from cell A onto cell B keeps cell B from firing at the beginning of its response,
which is at the end of cell A's response. Note that the inhibition has a slight delay relative to the activity of its source, due to filtering.
Once cell B starts firing, it is no longer receiving inhibition because cell A is inactive. Only the onset is affected. This models the data, and reminds us that timing is important.
Panel B shows the responses that the structure in A produces. The space-time maps show that the left and right simple cells receive spatiotemporal quadrature inputs from LGN.
Adding the mutual inhibition at the bottom of panel B has the effect seen above where the onset of the response is reduced, but here only at certain spatial positions because of the quadrature.
The receptive fields are given an orientation in space-time, which is the same as being direction selective. The cells share the same space-time orientation, with responses coming earlier in time moving from top to bottom in space.
This model is based on spatiotemporal quadrature, so it is unsurprising at its core. However, people have the intuition that a direction selective cell must be inhibited by cells that prefer the nonpreferred direction,
so a cell that is selective for downward motion is inhibited by cells that respond to upward motion. There is little evidence for that arrangement, and it doesn't make sense for simple cells because the timing would not match systematically for cells with opposite space-time orientations.
Timing must be taken into account when trying to understand neuronal processing!
In addition, the model uses feedback, which tends to be difficult for people to process intuitively. Electrical engineers are highly conversant with feedback, which is fundamental to the way that amplifiers work, for example.
Population biologists know that ecological systems depend on feedback between species occupying the same niche. Much of the richness of the brain arises from the massive feedback in its circuits.
Evidence for the model in Figure 39 comes from several excellent studies that measured space-time receptive fields while deriving the contributions of excitatory and inhibitory inputs.
Murthy and Humphrey showed that inhibition is tuned in the same direction as excitation (see their Figure 12).
Priebe and Ferster provided strong support by measuring excitatory and inhibitory receptive fields, showing that they were in quadrature (their Figure 6).
Monier at al. wrote that "a majority of cells showed both excitation and inhibition tuned to the preferred direction".
Znamenskiy et al. demonstrated that excitatory and inhibitory neurons in mouse visual cortex with similar response properties are connected.
Lien and Scanziani also provided results on geniculate and cortical responses in mice consistent with the model proposed above.
Kuo and Wu found a related organization for direction selective auditory neurons in the inferior colliculus.
Our model is broadly supported, although objections are sometimes made based on ignorance of phase.
Livingstone claimed that lagged cells are never biphasic (transient), meaning they don't have absolute phase values near 0.25 c.
This is of course not true, as shown by the examples above and the scatterplots of absolute phase values. Ralph Freeman claimed that lagged and nonlagged cells differed in phase by a half-cycle.
The claim seems to be based on the distributions of latencies of lagged and nonlagged cells.
As with Livingstone, they apparently thought that lagged cells were all monophasic (sustained; see the biphasic transient lagged cells above or Fig. 11 G,H in Saul & Humphrey, 1990).
Alan Freeman argued that the relative delay between lagged and nonlagged responses would not suffice to produce direction selectivity, completely ignoring the phase differences.
Chariker et al. (2021) modeled direction selectivity
in macaque visual cortical neurons based on temporal response differences between ON and OFF cells.
They claimed that lagged and nonlagged input can not explain macaque direction selectivity.
They argued that the differences between the temporal frequency dependence of direction selectivity in monkey and cat invalidates the dependence on lagged and nonlagged cells.
As described above, the opposite is true: the difference in temporal frequency tuning of direction selectivity is matched by the differences in LGN absolute phase and latency.
Furthermore, they claimed that "lagged cells have not been found in macaque LGN", ignoring Saul (2008).
Priebe and Ferster showed the clearest evidence for our model, but denied it because they refused to think in terms of phase, and didn't understand why excitation and inhibition are tuned in the same direction.
They wrote: "In this paper, we provide evidence that the excitatory and inhibitory synaptic inputs to simple cells prefer motion in the same direction, which is the direction that evokes the most spikes.
While excitation and inhibition were tuned to the same direction, the two components were evoked asynchronously by moving stimuli. This difference in the timing of excitation and inhibition appeared in responses to simple gratings as a 180° phase difference between the excitatory and inhibitory inputs."
That last sentence applies of course to motion in the preferred direction. They did not consider the relationship between excitation and inhibition for motion in the nonpreferred direction:
"Our results suggest that inhibition plays little role in shaping direction selectivity in simple cells. It is unclear, however, why inhibition should come from the same direction as excitation".
They too were stuck on latency: "Most models of direction selectivity are based on input that differs in latency for different spatial positions".
I had repeatedly attempted to show David Ferster how direction selectivity works in our model, but he never accepted my reasoning. I attribute this to a prior belief that inhibition is not important, and a difficulty in understanding phase.
This is common among the many people I've talked with about direction selectivity, and a prime reason why I wanted to lay this out here.
The question (of most interest to me) arising from thinking about neurons that are sensitive to direction is how do they get that way?
Our neurons combine signals from other neurons that differ in time and in some other property in order to signal a change in that property over time. We can't have neurons that do this trick for every possible property and time scale.
Instead, we learn to detect directions in which things that matter change.
The key neuroscientific idea that we use to explain how the brain learns things ("plasticity", the ability of the brain's function to be modified) is often attributed to Donald Hebb, a psychologist, who argued that neurons become more likely to respond to input from other neurons when their activity coincides in time.
Hebb proposed that learning occurs in the brain through coincident activity in a presynaptic cell that contributes to activating a postsynaptic cell. The neurons are connected by synapses, and the strength of these synaptic connections might be modulated by the coincident activity.
Hebbian synapses are strengthened when the presynaptic and postsynaptic activities happen at the same time. Hebb's phrase describing this is that "neurons that fire together wire together".
A tremendous amount of work has shown that Hebb's general idea is realized in various forms in actual brains. The numerous results are too complicated to be summarized here, but we will give some relevant examples. One of these is called "spike-timing dependent plasticity", or STDP.
It provides a useful example on several levels.
An important bit of background before describing STDP is to first know about LTP and LTD, "long-term potentiation" and "long-term depression". LTP was discovered first, and remains the keystone for our views about Hebbian plasticity.
The experiments use one set of output neurons that can be excited by another set of input neurons. First, the degree to which stimulating the input neurons excites the output neurons is measured as a baseline.
Then, the input neurons are very strongly stimulated, which excites the output neurons very strongly. Following that strong conditioning stimulation, the original measurements are repeated, with the weaker stimulation that was used to measure the baseline activation of the output neurons.
What was observed in certain sets of neurons was that the response of the output neurons was potentiated, made stronger relative to the baseline, following the conditioning, just as Hebb predicted.
After only seconds of strong conditioning, this potentiation persisted for hours with no further conditioning, and so was termed LTP. An interpretation is that this might be the basis of learning and memory, that a brief experience can lead to a persistent increase in responsiveness when the triggers for a memory are experienced.
This is analogous to how using our muscles during exercise leads to long-term improvement in our strength.
LTD was observed later. One experiment showing LTD was modeled on the LTP experiment, but instead of conditioning with a strong input stimulation, the inputs were stimulated more weakly than usual, and subsequent testing produced weaker than baseline activation of the output neurons.
The conditioning in the LTP experiments consisted of seconds of stimulation, producing hundreds of action potentials, usually in many neurons simultaneously. In order to try to decipher what mechanisms are involved in these forms of plasticity, more precise experiments were attempted,
reducing the problem to what happens when single action potentials ("spikes") are produced. Potentiation can be generated by pairing a single spike in a single input neuron with a single spike in an output neuron, at least when this pairing is repeated enough to produce changes that are large enough to be detected.
If the two spikes that are paired are simultaneous, potentiation is generally seen. In the brain, however, there is often a latency of several milliseconds between input and output activity, for various reasons, especially the need for temporal summation of the inputs.
So experiments were designed to vary the latency between input and output. These STDP experiments indicated that potentiation is observed when the input precedes the output by up to tens of milliseconds, as one would expect to occur in the brain.
When the input instead occurs after the output, which might not be expected if the input activity is causing the output activity, depression was observed.
Figure 41 (modified from Figure 7 in Bi and Poo 1998) shows the timing from this sort of experiment, with potentiation becoming stronger over tens of milliseconds for input preceding output spikes (Δt>0),
but reversing to become depression over tens of milliseconds for input following output (Δt<0).
Direction selective cells need to integrate inputs from other neurons that differ in space and time, as described above. As described in detail above, these inputs will fire at the same time (in phase) when stimuli move in one direction, but will not be synchronous (out of phase) for the opposite direction.
On average, assuming that the two directions of motion occur about equally often, the inputs should not be associated with each other, since their net correlation (in phase = 1, out of phase = -1, an average of 0) would be small.
However, as with STDP, synaptic changes typically depend in a particular way on activity in the postsynaptic neuron, the output. Synaptic changes are "gated" by the postsynaptic activity. This was termed postsynaptic resonance by Rauschecker and Singer (1979).
In the nonpreferred direction, the direction selective neuron is not activated, and so no synaptic change occurs. This permits the association because of the synchrony in the preferred direction (ARVO poster; Feidler et al. 1997).
If kittens grow up in an environment that is lit only by brief flashes 8 times a second generated by a strobe light, they don't experience smooth motion.18 Several labs showed that cats raised that way did not have as many direction selective neurons in visual cortex as cats reared with continuous lighting.
We showed that the spatiotemporal receptive fields of strobe-reared cats did not have the space-time oriented receptive fields associated with direction selectivity (figure 3 in Humphrey & Saul 1998).
Instead, the receptive fields were of the classic Hubel & Wiesel variety (figure 4 in Humphrey & Saul 1988), with different parts of the receptive field separated by half cycles.
Cortical simple cells in strobe-reared cats had regions with lagged or with nonlagged timing, but not in the same neuron. Allen Humphrey provided an explanation for why this is the case.
In a continuously lit environment, inputs with different timings can be associated onto a cortical neuron because moving stimuli cause those inputs to be active at the same time as stimuli move across the receptive field.
But with very brief strobe flashes, lagged and nonlagged neurons do not fire synchronously, because the lagged cells have longer latencies, and by the time they fire, the nonlagged cells are silent following their brief responses (figure 10 in Humphrey et al 1998).
This prevents neurons from having both lagged and nonlagged inputs.
We speculate that this is a general paradigm for how the brain sets itself up to behave adaptively. The relative timing of different inputs creates potential associations that depend on the timing relationships.
Associations are made when timing is right in a statistical sense, when the in-phase timings occur often enough and lead to some sort of reinforcement, generally meaning postsynaptic activity.
The result is that the brain is full of neurons that are selectively active for processes that occur in one direction in time but not the other. Muscles contract when we need to move in one direction, and relax when we move in the opposite direction, based on signals from neurons that fire in this direction selective pattern.
The world is not symmetric with respect to many of these processes. Things tend to fall toward the earth, in our experience. We might therefore expect that we have more neurons that respond to things falling down than up.
Experiments have been performed to suggest this is the case: raising kittens in an environment where visual movement is predominantly in one direction biases the visual cortical population toward responding to the experienced direction.
Below, we will rely on this idea to suggest why we think that time itself has a direction.
It's possible to lose direction, as well. A rare case of motion blindness was studied by several investigators. A woman known in the literature as LM had seemingly intact function after suffering a hemorrhage, but could not see visual motion.
As Josef Zihl, the scientist who studied her most, reported in a review paper (Zihl & Heywood 2015):
However, in most brains, timing is highly reliable. Comparing the reliability of neurons' responses in amplitude vs. timing, there is no contest: amplitude is notoriously unreliable, whereas timing is completely reliable, when measured in terms of phase.
Mechanisms like STDP might be responsible for allowing us to develop our exquisite timing. At least for people who can tell jokes.
A good example of how this way of looking at the brain can be useful comes from reinforced learning. We learn associations between a behavior and reinforcers (rewards or punishments). Typically, the reinforcer occurs in time after the behavior.
How does the brain put together the information from the reinforcement with the earlier information about the behavior? It is not uncommon to find explanations in the literature that violate causality, claims that the reinforcer extends back in time to influence the behavior.
The problem is particularly difficult because multiple behaviors typically precede a reinforcer, leading to the credit assignment problem. The solution, in part, involves realizing that the neuronal activity evoked by a behavior is extended in time.
This activity can lag the behavior, and persist to when the activity evoked by the reinforcer comes along. Working in the time domain makes it difficult to see the conjunctions in these spike trains. In terms of phase, on the other hand,
all that's needed is to compare phase values to see if the behavioral activity is in phase with the reinforcement activity.
These conjunctions are mediated in the brain by neurons that receive inputs from cells mediating the components, the behavior and reinforcement. When a behavior consistently precedes a reward, some neurons consistently receive inputs from lagged behavior-related neurons as well as from reward-related neurons,
and through Hebbian processes strengthen their responses to the stimulus.
A student who does her homework and later receives a good grade has her diligence reinforced by the grade. Presumably there are neurons related to her decisions to do her homework that continue to fire well after the homework has been completed and the grade has come along, so that the neurons related to the reward are firing at the same time.
This strengthens the association between doing homework and getting good grades. She learns that doing homework leads to rewards.
Goro Kato, a world expert on sheaf theory, and in particular cohomology, spent a year at WVU as a visiting professor, and asked me who I was at a Math Department meeting. Goro has an infectious cheery personality. He got me studying abstract algebra again, insisting on rigor that I have a hard time achieving.
Our friendship persists, and he has been my collaborator on the sheaf theory presented here, though my poor understanding leaves the presentation here lacking.
Sheaf theory is part of the most abstract work in Mathematics, Category Theory, often lovingly termed "General Abstract Nonsense". Sheaves were invented by Jean Leray when he was a prisoner of war in 1945.
From 1949, Alexander Grothendieck formulated increasingly abstract ways to think about numerous fields. Grothendieck was one of the greatest thinkers of all time. He had a fraught childhood, spending time in internment and in hiding during the war.
He rocketed to fame in Mathematics, producing a massively influential body of work. He was concerned about social and political problems, and did not go to Moscow to receive the Fields Medal (the analogue of the Nobel Prize, for Mathematicians) in 1966.
By 1970, he moved away from academia and its society, focusing on antiwar and ecological causes. He continued his work nonetheless, mostly publishing by writing letters to colleagues. He made known his concern about the ethics of the mathematics community, mostly in polite ways.
Spiritual matters grew important to him. He became a hermit in 1991, and died in 2014.
Goro's influence on my appreciation of sheaves has led to these attempts to apply this abstract mathematics to the brain. Other people have applied sheaf theory, mostly to network analyses, which have been proposed as an important way of looking at the brain.
Goro applies it to problems in physics and in consciousness. Neuroscientist Mike Shadlen's son Josh is a sheaf theorist who denied that this sort of abstract math could be applied to neuroscience.
As described elsewhere, the beauty of sheaf theory is that it provides the structure to analyze local-to-global transformations, as well as formalizing cortical structure and function as usually set in the context of columns.
We now consider the earlier introduction of receptive fields and sheaves (stalks over a topological base space, with continuity axioms) to unite these concepts, using direction selective receptive fields as a main example.
These receptive fields are described in terms of how they are structured in both time and space. Time and space are characterized as one- and two-dimensional19, respectively, in almost all accounts of visual receptive fields, and we will instead think of them in the frequency domain, in terms of phase and amplitude across temporal and spatial frequencies.
Our argument for why the brain is so smart is that it combines signals from neurons that differ along more than one dimension locally. For instance, neurons that differ in space and in time are combined to create novel neurons that are direction selective, and that are slightly more global.
By repeating this process many times, neurons develop quite elaborate response properties, and we are thereby able to perform complex tasks.
We will start by considering lateral geniculate receptive fields, because these are simpler than visual cortical receptive fields. In space, they are modeled as having a roughly two-dimensional Gabor shape (a Gaussian multiplied by a sinusoid, a "Mexican hat" shaped function).
That is, there is a central area that is either ON or OFF, and a surround with the opposing polarity (Fig. 42). Because these receptive fields have circular symmetry to a large extent, we can approximate their spatial organization with a single dimension, the radial extent from the center.
With that simplification, a one-dimensional Gabor is applied. In time, they have one-dimensional temporal kernels (transient, sustained, lagged). This is the conventional characterization of LGN receptive fields (Fig. 43, top row).
For the frequency domain representations, the kernels are simply multiplied by the stimulus to produce the response, and it is easy to view them as the filters, the actual regions of spatial and temporal frequencies where the neuron responds.
Both interpretations are easily made when frequency and phase are the dimensions.
Note that the space and time domain descriptions have fairly complex shapes that may be easy to look at and seemingly understand, but are difficult to describe in words or numbers.
The frequency domain descriptions are simpler, with Gaussian amplitudes and linear phase, with the slope of the phase vs. frequency line giving spatial and temporal offsets, and absolute phase providing a single number that tells us about the shape of the spatial profile and temporal kernel.
These receptive field models are sheaves, with the base space being time and space relative to when and where the stimulus occurs, and the stalks being the set of real numbers that correspond to amplitudes, as in Fig. 43.
For a particular LGN receptive field, the stalks take values corresponding to the Gabor function in space and the impulse response in time, or to just amplitude at each frequency and phase (Fig. 11).
Note that most stalks in the frequency domain have values near 0, because non-trivial amplitudes exist only at the frequency-phase values determined by their quasilinear relationship.
We now move to visual cortical (V1, primary visual cortex) receptive fields. These are constructed by neuronal connections from LGN to cortex as well as by intracortical connections. A worthwhile way to begin is to take a V1 neuron that receives inputs from just two LGN neurons.
These are excitatory inputs, and our first order approximation is that the V1 neuron just adds the contributions from the LGN inputs. Having two spatial dimensions complicates matters, but there is again a way to reduce this dimensionality.
V1 cells are orientation selective, meaning they respond better at a certain orientation in two-dimensional space than at neighboring orientations. This orientation, for our simplified two-input example, would be perpendicular to the axis through the offset centers of the inputs.
Note that motion of a contour is always perpendicular to its orientation, so parallel to the axis between the inputs, as in Movie 7.
Then, the space-time receptive field of the V1 neuron is the weighted combination of the impulse response functions (IRFs) in time, where the weights are given by the spatial Gabors:
A typical V1 receptive field, as documented by Hubel and Wiesel, looks like Fig. 44 (top), with offset ON and OFF zones. The ON and OFF polarities can be incorporated into either the Gabors or the IRFs.
LGN cells do not tend to differ much in spatial phase. Simple cells do, on the other hand, as in the example in Fig. 45,
where one simple cell (in red) has 3 subzones (OFF/ON/OFF) and the other (in blue) has 2 (ON/OFF).
Figure 45 shows receptive fields in both spatial and temporal quadrature, as illustrated in Fig. 40.
The two inputs each have two factors, a spatial receptive field and a temporal receptive field. These factors are separable, there is no dependence of one factor on the other.
Their sum, the direction selective V1 receptive field, on the other hand, does show a dependence on the temporal and spatial structures that can no longer be separated. It is inseparable in space and time: the timing differs across the spatial receptive field (or vice versa).
Inseparability is another way of viewing the emergent property of direction selectivity.
In terms of the sheaf, again, the two inputs have amplitude values above the frequencies/periods and phases (Figure 46 top).
The red and blue inputs here are in spatiotemporal quadrature. The figure only shows the temporal sheaf.
Almost one cycle of phase is included, from 100 ms (10 Hz) to 4 s (0.25 Hz).
The relative phases are a quarter cycle apart (Fig. 46 middle).
That quarter cycle is apparent at low frequencies (absolute phase) and the inputs have identical latencies (100 ms),
so the quarter cycle is maintained across frequencies. At low and high frequencies, the blue input has phase values that approach 0 c (to the right).
The red input approaches 0.25 c (up) at low and high frequencies.
The cortical cell combines these inputs, linking the stalks over distinct open sets that differ by a quarter cycle.
Although the frequency domain is less familiar, it is easier to interpret than the space-time plot in Fig. 45,
just showing the quarter cycle relationship that defines direction selectivity, keeping in mind that there is a similar spatial frequency sheaf.
Note also that the frequency domain makes it clear that there are important things going on at low temporal frequencies - these are hidden in the spacetime plots.
The neurons whose temporal properties are shown above also have spatial receptive fields. We made the two neurons to have quarter-cycle differences in space as well, and that plays into the morphism, making responses direction selective.
The illustrations here are of receptive fields in the early visual pathway. These are local processing elements, with only a small portion of space and time activating the neurons.
As the complexification process is repeated many times across the tens of billions of neurons in the brain, global concepts are created.
We perceive motion even when stimuli do not contain the cues we've discussed so far (that is, first-order motion). Second-order motion does not contain quarter-cycle differences in luminance.
Movie 14 is an example of such a stimulus. Motion here must be processed by neurons that have inputs that complexify the luminance signals to obtain temporal contrast across space.
These contrast differences are in spatiotemporal quadrature. The motion is often the cue that lets us see form: motion breaks camouflage.
In visual cortical area MT, almost all neurons are direction selective, and many respond well to higher-order motion as well as to first-order motion.
What the brain does to produce global concepts is thus a matter of the sequences of the morphisms of receptive field sheaves.
Analyzing the neural pathways in this way might allow a systematic view of the processing that makes the brain so smart.
At each point in the processing chains, some properties of the neurons are ignored,
and others are created by convergence of inputs with slightly different properties.
It is not necessary that this is hierarchical, and is certainly not purely serial or totally ordered.
One expects that aspects are somewhat hierarchical, in that the processes are likely to lead to increasing globalization.
In many cases, spatial location is ignored in order to recognize objects: this type of processing occurs in the ventral streams of sensory cortex.
But in the dorsal streams, those spatial properties are preserved and extended, and the object recognition is relatively ignored.
Providing a concrete example of these abstract concepts, we can go back to what was described above.
Let's start with retinal ganglion cells, with spatial and temporal receptive fields like those in Fig. 43.
These neurons respond to small flashed spots with either transient or sustained firing.
They project to LGN cells. Those cells can have receptive fields that are similar to their inputs,
but some transform their retinal input to generate approximately quarter-cycle phase lags (the Hilbert transform).
Putting together lagged and nonlagged projections to V1 simple cells (which are often postsynaptic to other simple cells as in Fig. 40) creates direction selectivity.
Simple cells with a range of spatial phases can then result in complex cells (which are often postsynaptic to geniculate inputs, at least partly bypassing simple cells).
Direction selective V1 neurons with differing spatial phases project to area MT to generate strongly direction selective cells with large spatial receptive fields, and that are sometimes direction selective for plaids, a second-order property.
We thus have a sequence:
RGC → XL ⊕ XN → ∑DS S → ∑DS C → MT
By considering each step in these chains, we obtain a more precise characterization of the mechanisms at work in the brain that create emergent properties.
Timing is altered in the lagged cells at the first morphism.
Direction selectivity emerges next. Spatial generalization happens over the next two stages.
The examples here have often been greatly simplified to employ two inputs to one postsynaptic cell that appears to be above the inputs on a hierarchy.
In fact, the brain is a complex network.
Each neuron typically receives many inputs. Simple and complex cells receive both geniculate and cortical inputs.
We could model the real situation as a sheaf that is a sum of all of these inputs.
In addition, as modeled in Fig. 40, neurons feed back on each other. The network is not simply feed-forward up a hierarchy.
In sheaf theory, many diagrams are feedforward, but feedback is also studied.
Feedback often tests our intuition, as might be apparent from Fig. 40.
19 Two-dimensional visual space is widely studied, The third dimension of space, depth, is also studied. Depth is not derived the same way as the horizontal and vertical dimensions, which arise from the structure of the retina as a sheet.
Depth arises from a large set of cues, with most attention on stereopsis, where differences in horizontal spatial phase between the two retinae provide a fine sense of depth.↩
Most of the motion that we experience arises from our own movement through the world. Eye and head movements are an important source of self motion. We discussed earlier how the brain might deal with rapid eye movements.
A broader, more general view of self motion might inform our view of how the brain uses sheaves.
Take two objects in your visual field. Look at one of them, then quickly look over to the other. Repeat this and think about what happens when you make these saccades back and forth. Did the objects appear to move with each eye movement?
They were more likely fixed in space and did not move across the wall or floor or outdoor scene. They did move across your retina, however, and you may not have had a sense of that movement.
As opposed to when you see an object that is moving across space, self motion moves the entire world across the retina. Your brain uses that information to distinguish self motion from object motion.
The visual effect of self motion is optic flow, or global motion, with most of space moving in roughly the same direction.
Filmmaker John Whitney used optic flow to stimulate our visual systems, and Doug Trumbull used Whitney's techniques to provide that kind of stimulation in 2001: A Space Odyssey.
Motion of large parts of the visual scene across the retina (Movie 16) activates a group of direction selective retinal ganglion cells that projects to areas at the base of the brain.
This basal optic system, often termed the accessory optic system (AOS), has several nuclei that differ in preferred direction of motion, mostly vertical (up and down) and horizontal (primarily from temple toward nose) directions.
These neurons and their projections to brainstem nuclei mediate the optokinetic and optomotor responses, by which we move our eyes and head to reduce the optic flow when we move through the world, enabling us to see objects by keeping them from moving across the retina and near our center of vision.
The receptive fields of accessory optic neurons are very large. They are presumably built from the projections of many direction selective retinal ganglion cells originating from widespread retinal locations and having large receptive fields themselves.
As described above for the V1 to MT projection, spatial localization is discarded in the retina to accessory optic system projection. These transformations permit behaviors that are influenced by the entire visual field, global in the sense of something that is happening everywhere in space.
Smooth pursuit eye movements are made when we track a small object that moves through the visual field. For example, we may keep our eyes on a bird flying across the sky.
The visual stimulus in this case is the object that we want to keep centered on our eyes plus a background that moves across the retina.
It has both a global component and a local component. Area MT is one of several cortical regions that are important for mediating the behavior that lets us track the object.
The brain uses error signals for most sensorimotor processes, and here the error signal is called retinal slip.
When the object being tracked moves away from the fovea, a velocity signal is provided to the motor system by direction selective cells.
That signal enables eye movements to reduce that velocity toward 0. Most studies have emphasized how the brain generates the motor behavior that controls eye movements.
The sensory perception depends on both discarding localization to produce the optokinetic reflex, and direction selective cells with small receptive fields that monitor how well the object stays on the fovea, the center of the retina.
An important type of spatial transformation works in a different way. In parietal cortex, where MT resides, spatial processing is emphasized. Visual processing in the early visual pathway is retinotopic, meaning that receptive fields are localized on the retina.
In AOS, this localization is lost. In MT, it is diminished. In other parietal areas, such as LIP, retinotopy is replaced by other mapping strategies.
Our perception is clearly not retinotopic: when our eyes move, the world does not move with the retina. The results presented earlier, about how the LGN shifts neuronal timing starting before saccades are executed, is an example of how the brain breaks away from retinotopy.
In LIP, a remapping of space seems to occur around saccades. Before a saccade is executed, some LIP neurons shift their receptive field to the location from where a stimulus was before the saccade to the location where the stimulus will be after the saccade occurs.
That allows these neurons to respond more continuously to the stimulus across the saccade, as suggested by the timing changes we saw in LGN.
One might guess that the entire map of the visual field is shifted. That may not happen. LIP is an important part of a large network that mediates attention, and it is possible that only what we are attending to gets remapped. We don't care so much about the rest of space, we only care about where we are looking.
Thus, what LIP does is a great example of the sheaf morphisms we've discussed. A lot of information is thrown away, with a gain of information about what we care about. This is a kind of rejection of globalization.
In temporal cortex, down by our ears, spatial localization tends to be discarded in a really important manner. Cells in this part of the brain can have amazing stimulus specificity. Faces are an example. There are neurons that respond specifically to a familiar face (and sometimes to other representations of the bearer of the face, like their name).
These neurons will respond to their preferred face without regard to how the face is oriented or where it is seen in visual space. The size of the face doesn't matter. A lot of information is nulled out in order to process what does matter.
These examples of globalization all point to analyses in terms of phase as the way to understand what's going on. As what counts is how local elements are related to each other, as opposed to where they appear on the retina or other sensory peripheral organs, that relativity is captured by phase.
Faces are a great example, with elements like eyes that are found relative to other elements like each other and the outline of the face. We give directions this way, sometimes indicating that an object is at 2 o'clock, or that we need to go up and to the left.
We take ideas from numerous sources, and put them together to generate novel ideas. A chef might combine disparate ingredients from several geographic areas to create new dishes that meld related and unrelated flavors. An architect collects building designs and finds new ways to surround spaces.
Inventors assemble ideas into devices and other products that can change millions of lives. Populations arise from two cells.
We now extend our earlier discussion of how our behavior depends on timing. We emphasize that timing is primarily used to tell us about direction. But there are other aspects of behavior that are not obviously about direction.
Although we often think of our actions as happening at a moment in time, in fact they are a product of a series of actions occurring over a duration, and are better thought of as a process.
If a soccer player scores a goal, it involved many behaviors and billions of neuronal and muscle activations, for instance a set of passes, individual moves, planning, reacting, creating, and following through, including celebrating.
Getting hired for a job is not a momentary act, and involves not only the lengthy preparation needed to attract and qualify, but also the performances of the employer and employee once the job begins. That may be obvious, but on shorter time scales the same timings happen.
If you push a button, you are making movements before and after the button press.
You may have seen people who speed toward a red light, braking only as they get quite near. It seems common to find people who can't seem to do things ahead of time. They do not get ready to get out of the car until they've already reached their destination.
They don't start cooking for a big meal until it's almost time to eat. They rarely arrive anywhere early, and are frequently late. Despite often making other people wait, they are impatient if they are left idle for a few minutes.
We speculate that their brains are impoverished in "transient" mechanisms. These are cells that are active ahead of the peak of some process, with phase leads. Such mechanisms can prepare us to act ahead of time.
An opposing problem involves difficulty sustaining behaviors, and thus losing focus, attention, persistence, etc. Perhaps "sustained" mechanisms, having phases that match the processes related to their activity, are somewhat lacking in people with these problems.
ADHD is characterized by the need for immediate reinforcement of behavior. An illustration of this finding appears in Figure 7 of (Sagvolden et al., 2005). This figure seems to argue that the reinforcer acts backwards in time to interact with the response.
Such non-causal explanations are easily rejected. As Sagvolden et al. explain, and as touched on above, what is presumably going on is that the responses activate neurons, and if that activity persists until the reinforcement is provided, synaptic modifications occur that alter future behaviors.
The difference between the ADHD and typical populations might thus be a matter of how long activity persists. Lagged timing means that responses come during the fading phase of a process. This timing is crucial to enable overlapping activity evoked by a behavioral response and by a reinforcer.
Such simultaneous activity is needed for learning. A lack of lagged timing implies difficulties with delayed reinforcement.
An easy case for remembering these timings involves sex.
Human sexual behavior often consists of a buildup phase of foreplay, a phase with a climax, and a dénouement of cuddling and loving winding down.
A lack of transient mechanisms would correspond to disinterest in foreplay.
Without sustained mechanisms, premature ejaculation could occur. A person lacking lagged cells might be done with the whole thing after climaxing.
In fact, almost all behaviors work this way. They are processes that build to some sort of inflection point where they wind down. Baseball batters ready themselves for a pitch, and as they decide they might swing they go into motion. If they continue their swing they attempt to move the bat into the direct path of the ball.
The follow through lets their energy dissipate smoothly. Each of these components is needed for a successful behavior.
This is a simplistic view of what are likely to be complicated behavioral issues, but may be helpful in understanding some of the etiologies. In the extreme, we have the disorders discussed above, like ADHD and the learning disabilities studied by Tallal.
A wide range of abilities and disabilities can be found across age and other factors. Adolescents appear to retain poor timing abilities, for instance. In cat, we showed that timing develops quite late, compared to spatial processing (Saul & Feidler 2002).
These individual differences must arise from brain mechanisms. Timing is generated almost everywhere in the brain, but one of the areas that could underlie many of these differences is the thalamus.
The thalamus consists of about 60 nuclei that receive inputs from different parts of the brain and project to different cortical areas.
To a large degree, inputs to cortex come from thalamus. Many neuroscientists think of thalamus as simply relaying their inputs on to cortex, but thalamus does its own processing before the relay. The work of Mastronarde revealed the key change in timing that visual thalamus provides.
The triadic circuitry that creates lagged LGN cells is present throughout thalamus, and seems poised to provide similar changes in timing for audition, somatic sensation, emotions, motor processing, cognition, and much of what cortex does.
Thalamic neurons differ in their timing: transient, sustained, and lagged timings form a complete coverage of timing, characterized by absolute phase.
Thalamic neurons exist with all absolute phase values. However, the numbers of neurons with each absolute phase value differ across individuals.
We propose that reduced numbers of transient, sustained, or lagged neurons can cause the atypical behaviors described above. These thalamic neurons may be sensitive to developmental alterations that create the individual differences in timing.
Although thalamus is emphasized here, other brain regions are undoubtedly important as well. Cerebellum is a particularly compelling place where timing is key. The cerebellum interacts with the rest of the brain to modulate our behaviors, emotions, and practically every function.
These modulations generally consist of regulating timing, for instance to make our movements smoother.
One of the heavily studied cerebellar functions is eyeblink conditioning. A brief puff of air is delivered to the eye of an animal subject. This causes the eyelid to close, a blink. That is an unconditioned response, a mechanism that protects the eye.
This reflexive response can be conditioned, for instance by playing a sound before the airpuff. When the sound is repeatedly heard prior to an airpuff, the subject blinks after the sound but before the airpuff itself.
As conditioning proceeds, the subject improves when the blink occurs, the timing of the conditioned response (Figure 47).
Damage to the cerebellum prevents this improvement.
Note that the Purkinje cells are inhibitory, and have a high maintained firing rate (spikes shown in b and c).
The conditioning leads to a pause in Purkinje cell firing prior to the airpuff, permitting their targets in the cerebellar nucleus to respond.
LTP increases Purkinje cell firing rates, and thereby suppresses activity in the nucleus cells. LTD has the opposite effects.
Another good example of how the brain modifies our behaviors involves how we maintain our gaze on an object when we're moving. This was discussed above. When we walk, our heads move around. This would be expected to make it hard to see what we're looking at.
But several mechanisms stabilize our vision. The vestibulo-ocular reflex (VOR) takes signals about how our head is moving, and feeds that to our eye muscles to compensate for the head motion. If your head turns toward the right, your eyes need to turn to the left to keep looking where you want.
We also use the signals from the accessory optic system that arise from "retinal slip", the visual signal that the eyes are not stabilized.
When your head turns to the right, the world moves to the left. The visual system computes the speed of that motion and tells the eye muscles to move the eyes at that speed to match the retinal slip.
This is the optokinetic reflex (OKR).
Ideally, these mechanisms would compensate perfectly for our head movements. That compensation is measured by "gain".
Gain is the ratio of eye movement output to head movement (for VOR) or retinal slip (for OKR) input, as in audio amplifiers
(turning the volume knob of an amplifier changes the gain, controlling how loud the output sound is).
Perfect compensation in our case means a gain of 1, so the head movements are exactly compensated by eye movements. Neither the VOR nor the OKR has a gain of 1, however. The gains of these mechanisms depend on the temporal frequencies of the head movements.
The OKR approaches a gain of 1 at low frequencies, whereas the VOR has a low gain at low frequencies and a higher gain at high frequencies (Figure 48).
Together, their gains add up to something near 1 across frequency (Schweigart et al, 1997).
What counts, of course, is timing. The numerous granule cells are activated at different phases of the head movements. LTD adjusts the strength of the synapses from the granule cells onto the Purkinje cells dependent on the phases. The cerebellum generates exquisite modulations of the basic VOR by manipulating the timing of the inhibition onto the vestibular nucleus cells.
The OKR is similarly modulated by the cerebellum. Visual retinal slip signals activate different granule cells, and LTD tunes Purkinje cells to supervise the gain of the reflex. Together, VOR, OKR, and their cerebellar controls enable us to maintain visual function and not experience the kind of disruptions we get from unstabilized moving cameras.
Most of our skilled behaviors rely on learning those skills based on cerebellar mechanisms. Playing music, sewing, speaking, processing emotional issues, solving puzzles, and all the other amazing things we do, are generated by processing in various parts of the brain, but cerebral cortex has a large responsibility, and cerebellar cortex massages our actions to make them beautiful.
Another lesson from the workings of cerebellum is that the cerebellar nucleus neurons that receive the inhibition from Purkinje cells can be thought of as having been programmed to generate some behavior. They can't execute this behavior, however, until the inhibition goes away.
This is a common strategy. Certain inhibitory neurons have high firing rates, and keep their targets from firing. Only when the inhibitory neurons pause their firing are their targets released, and a behavior is executed.
The best example of this comes from saccade generation. The superior colliculus in the midbrain programs saccades, determining their direction and amplitude.
Inhibitory omnipause neurons in the brainstem keep the saccade from starting until they pause, at which time the eyes move in a partly ballistic fashion, meaning without further guidance, until the eyes reach their target.
The inhibition sets the timing of these behaviors.
My speech therapist told me a story about a young patient who was having serious behavior problems. They decided to equip the child with a smart watch that reported his heart rate. His foster mother monitored him this way, and had him jump on a trampoline at a certain time when he needed to exert himself.
She also delivered shoulder rubs at other times. Keeping track of his behavior over time led to improvements in his behavior. This is a great example of what time is: it's when we do things, feel things, and think things. When we're thirsty, we drink. When we're in a bad mood, we act out. When we're tired, we sleep. When we're thinking about time, it's about time.
Time is of great interest to physicists, and excellent books have appeared recently describing the physical notions of time.
The authors touch on neurobiology to various degrees, but of course do not go into much detail.
What is most striking, however, is their reliance on one-dimensional time.
They take it for granted that time should be measured as points on a line, even though they show clearly that such a project leads to great difficulties.
Even the excellent We Have No Idea, by Cham and Whiteson, neglects two-dimensional time,
despite their coverage of the problems we have in understanding time.
Newton differentiated true time from relative time.
"Absolute, true, and mathematical time, of itself, and from its own nature flows equably without regard to anything external,
and by another name is called duration: relative, apparent, and common time, is some sensible and external (whether accurate or unequable) measure of duration by the means of motion,
which is commonly used instead of true time; such as an hour, a day, a month, a year."
Time is truly relative, however. By casting analyses in terms of phase, one automatically ensures relativity.
Richard Feynman talked about vision in terms of the physical makeup of the light that affects the eyes.
He described the vast variety of waves that make up the electromagnetic fields surrounding us.
The complexity of the physical world overwhelms our senses. Feynman reveled in the magnificence of our ability to make some bit of sense out of this massive array of frequencies and phases.
What our nervous system does is provide a huge amount of filtering, concentrating on the frequencies of interest.
Feynman gives the example of a pit viper's sensitivity to infrared frequencies, making it possible to sense the presence of its prey.
Very little of the complexity of the world makes it into our brain activity, let alone our consciousness.
Feynman loved most to think about everyday processes and try to understand what was going on.
For example, he reduced a lot of phenomena to the molecular level.
Heat is exactly the motion of a large population of molecules. As the molecules move faster, the temperature rises.
Again, it's all about timing.
The Heat Equation describes how heat moves through space over time. If you heat up a small area, over time the temperature rises at nearby locations.
The change in temperature depends on the difference between the temperature at any point and the average temperature surrounding that point.
The speed of the molecules at the chosen point changes depending on how they are affected by the speeds of the neighboring molecules.
It's like how people are influenced by their neighbors. And numerous other processes work this way. Think of the speeds of cars on a highway.
Or springs: when you pull molecules apart, they try to get back together. These are all examples of emergent properties,
arising from relationships involved in interactions among many molecules or other small elements.
The solutions to the Heat Equation are functions of space and time. Most of physics concerns how things change over space and time.
The Wave Equation has solutions that are waves moving through space over time. It describes vibrations of strings and other ways of producing sounds,
as well as the sounds traveling to our ears. Schrödinger's wave equation describes the behavior of electrons moving around the nucleus of an atom.
Waves are an emergent property of their substance. The molecules or other elements that make up the wave do not move with the wave as it progresses along space over time.
Instead, the elements change their temporal phase differently depending on their spatial phase. You can see that in a rope that you move up and down at one end,
to produce a wave that moves toward the other end. The parts of the rope only move up and down, taking on different phases of that up-down dimension.
The Diffusion Equation is equivalent to the Heat Equation under certain circumstances. It explains how a population of molecules diffuses, spreads apart.
So it is the same as how heat spreads when the heat just depends on the density of molecules.
If the molecules react with each other, you get a reaction-diffusion equation.
That is the type of equation that describes the waves Ken Showalter and I studied in the iodate-arsenous acid system.
It also can be applied to action potentials in neurons, and many other aspects of neuroscience.
I regularly get scintillating scotomas,
caused by waves of activity traveling across my primary visual cortex.
The dominant trend in 20th century physics was reductionism. By examining the world at smaller scales, the behaviors of the particles that make up matter became clearer.
The philosophy involved the idea that one could understand how matter behaved at larger scales by building from the knowledge about the small scales.
Increasingly powerful particle accelerators have been built to enable glimpses of increasingly high energy processes at increasingly small scales.
This philosophy has its merits, but has the weakness that behaviors at larger scales typically arise from emergent properties that aren't inherent in the small-scale analyses.
In neuroscience, it became apparent early on that studying the nervous system at a wide range of scales yields more knowledge
(Figure 49; Juavinett).
In biology, the primary division is between structure and function. Anatomy is the study of structure, and physiology of function.
However, the oxymoronic term "functional anatomy" has an important place.
People often hope that knowing the structure of something will predict its function. That hope is quite often dashed.
Structures commonly perform a variety of functions, and different structures can mediate the same function.
Conceptualizing time as points on a line tends to be reductionist, and thinking in the frequency domain can be more wholistic.
The frequency domain by definition encompasses all scales, whereas the time domain usually focuses on the smallest scales, at least in neuroscience.
We mentioned above that nothing can go faster than the speed of light. Why is that the case?
It is not intuitive that there should be a maximum speed, and why should it be the particular speed at which light travels?
This is a fascinating fact of nature. The speed of light has a finite value, but behaves asymptotically.
That is, it can be approached but not reached by anything that has mass. To accelerate mass, it takes energy,
and as the speed approaches the speed of light, it would take an infinite amount of energy to reach the speed of light.
In the sense of attaining it, the speed of light is infinite. Massless particles (photons) move at the speed of light.
If the speed of light were actually infinite, on the other hand, everything would happen at once. There would be no time!
We would see the whole universe at once, nothing would appear to change.
Lorentz showed that time dilates, that is gets longer, as the speed of something approaches the speed of light.
At the speed of light, time becomes infinite.
That is, periods are infinite, and the frequencies are all 0: nothing changes (hen ta panta, in Parmenides' Greek).
The finite speed of light is analogous to the finite temperature of absolute zero.
At that temperature (about -273°C), nothing changes. That is, no molecules move. Heat is exactly the motion of molecules.
Entropy is minimized, there is no disorder. Absolute zero can only be approached asymptotically, and not reached.
Somehow our intuition is violated less by absolute zero than by the speed of light.
And we have even better intuition about zero frequency, which similarly can not be reached, but is routinely characterized as DC, direct current, in electronics.
Note that the speed of light does not change in different "reference frames".
That is, no matter how, where, and when photons are generated,
they alway move through space and time at the same speed (until they are absorbed by matter).
Whereas if you throw a ball from a moving car it will have the sum of the velocities of the car and the throw,
the light coming out of the headlights of a moving car moves at the same speed as when the car is not moving.
This is true even if the car was moving close to the speed of light.
This deviates from our intuition, but makes sense from the relativistic viewpoint.
The color of the light coming out of the headlights of the moving car is affected by the car's velocity, however.
We're more familiar with how pitches change when a siren is moving toward or away from us.
If an ambulance is coming toward us, the pitch rises, and if it moves away, the pitch has lower frequencies.
Because galaxies are moving away from each other, their light is shifted to lower frequencies, corresponding to longer wavelengths.
That makes their visual spectra redder, so this phenomenon is called the red shift.
The photons emitted by the galaxies have less energy.
If the galaxies were moving relative to each other near the speed of light,
the red shift would make the frequencies of emitted light fall to near zero, so the wavelengths of the light would be extremely long.
Early on, we mentioned Nominalism, a philosophic view that rejects abstractions. In college, I had been exposed to Linguistics.
The professor for this course, Bozena Henisz Dostert, spent the first term in her home country of Poland,
and her newlywed husband Fred Thompson took over the teaching.
Thompson had diverse training and interests, having studied with Alfred Tarski,
and worked in computer science. He developed natural language abilities in computers, which at the time were not really capable compared to what we have now.
He taught Noam Chomsky's theories on syntax and philosophy, and I later did an independent study with him that I wanted to be about structuralism,
but he made it primarily a deep dive into Nominalism (Nelson Goodman and Willard Van Orman Quine).
Some, but certainly not all, of Chomsky's ideas came out of Goodman and Quine.
I was slow to appreciate the good parts of Nominalism, but am now committed to avoiding categorization of people.
In any large population of humans, there will be a large variance in almost any characteristic,
usually comparable to the variance across different populations.
This means that saying that one population is different from another is wrong.
For instance, mean IQ might differ slightly between men and women, but is not significant because of the large variance in IQ across both groups.
Randomly picking a woman and a man is not going to result in any consistent difference in IQ.
Rejecting abstractions can be difficult in general. Our brains generalize from our experiences,
providing us with the means to make categorical decisions.
These are beliefs that we should try to question whenever possible, however.
Abstractions give us a lot of power to understand the world, but often delude us,
because they don't correspond to any physical objects. We can't say that "red" exists on its own,
it only corresponds to perceptions about red things. The abstract sense of time similarly doesn't imply existence of time,
and arises from our experiences with the world changing in various directed ways, like growing up.
Buonomano discusses the term "mental time travel" at length.
This is the idea that the past and future are imagined for adaptive purposes.
It presents problems when viewed from the perspective of the timeline and its focus on the supposed present.
But knowing that we have nonlagged and lagged neurons makes this transparent.
The brain anticipates future behaviors by having phase leads, and responds to the past by having phase lags.
Current activities retain a link to the future through the phase lags, so that future reinforcements can be effective.
Temporal discounting, the fact that future reinforcements lose effectiveness with distance from the behavior that produces them,
simply depends on the decreasing activity of lagged cells, as illustrated by Sagvolden.
Neuronal activity is ongoing across time, and our brains therefore have information about the past and future built into that activity.
Nevertheless, we have great difficulty understanding very low frequencies. The distant future and past remain challenges to our cognitive capabilities.
Most neurons adapt to things that don't change quickly, and stop responding.
I wonder whether there are neurons that maintain activity across currently unimaginable periods.
Our oldest memories represent an example of neuronal activity spanning many years.
Cham and Whiteson give some examples of definitions of time. One of them approximates the view here:
"Time is what tells us when things happen."
Closer would have been "when things are happening." Whereas they characterize space as "goo", malleable across its extents,
they hardly recognize that time is gooey across its extents.
Things happen over periods of time, and what counts are the phases over the periods/frequencies.
These authors also discuss time in terms of the filmstrip model, although they emphasize continuity afterwards.
But whereas they describe a sheaf-type model for space, they fail to do so for time.
They see time as linked snapshots, rather than the two-dimensional topological space upon which everything changes.
The open sets of time are clearly interconnected locations when viewed as the disk, but not as the line.
Both space and time are best viewed as two dimensional, using frequency and phase. This implies that spacetime,
which is usually thought of as 4-dimensional, is actually 8-dimensional. This is certainly difficult to visualize,
but is easily treated mathematically.
Rovelli (The Order of Time and Reality is not what it seems) provides excellent analyses of why time doesn't exist. His context is quantum gravity.
He explains how space and time are quantized, and the quanta they are made of are linked to neighboring quanta.
Rather than existing in some hypothetical but non-existent framework of space and time,
the universe is built on these quanta. At the quantum level, the structures that produce time do not have a direction.
Just as we think that we are hitting the keys on our devices,
rather than just getting close enough to create electromagnetic forces,
we think that time exists as some flowing entity.
Time, like most things we believe exist, is a delusion. A delusion is a belief that is not true.
Our beliefs come out of our experience, and we think they are justified by evidence.
We are sure that our beliefs are true, but they are not justified by evidence, and so are not true.
Our beliefs originate in the workings of our brains.
The adaptive value of having beliefs is presumably that we need to make decisions without having all the evidence.
If we are driving and need to make a turn against traffic, we scan the roads and try to determine if it is safe to turn.
But we also take into account our prior experience. After a variable amount of time, we decide that it is likely to be safe to make the turn.
Every once in a while, our belief that it is safe turns out to be false.
In other words, mistakes are always cases where our beliefs are false.
Accumulating more evidence makes it less likely that we will make a mistake,
but there are no guarantees.
The prior experience is a particularly important part of beliefs not being true.
Most of the time, we don't have the time to accumulate enough evidence, and must make a guess.
Educated guesses are enabled by having lots of past experience that can guide present decisions.
Through experience, we develop intuition, and often rely heavily on that intuition.
That intuition tends to be useful and correct, but sometimes fails miserably.20
Being deluded about everything constitutes our normal state of being. This is neither good nor bad.
We think we feel time flowing by, which is seldom harmful.
Belief is adaptive, a very good thing. But wherever possible, we should check our beliefs, and be skeptical,
rather than blindly accepting what we think we know.
Common sense remains a great thing, but is not necessarily grounded in the realities of our extremely complicated world.
Cham and Whiteson make this point repeatedly in the context of the weirdness of physics.
The ways our brains work are at least as weird, creating our behaviors, emotions, movements, perceptions,
and thoughts from mechanisms that arose through hundreds of millions of years of adapting to varying environments.
We encounter novel environments, however, and often sense and do the wrong things.
This is especially clear in science. Scientists are continually coming up with ideas about what might be true.
Almost all the time, they are deluded.
One of millions of examples is how Einstein held for years to his belief that the universe was static, when in fact it is expanding.
A good scientist always tries to show that her beliefs are not valid. Most actual scientists unfortunately don't work that way.
We champion our ideas, often at the expense of not revealing the truth.
Time is not alone as a basic physical concept that we don't understand (see Cham & Whiteson, Rovelli, Feynman, Smolin, ...).
Space is also different from what we normally think about. Properties of elementary particles like charge, mass,
and spin do not correspond to anything satisfying. Gravity is a mystery.
Physicists continue to look for interpretations of quantum theory. The universe is full of mysteries like dark matter and dark energy.
So we should not feel frustrated about being deluded. Everything we know is wrong, or flawed.
On the other hand, Rovelli frames a cogent analysis in terms of quantum gravity.
His conclusion involves seeing time in terms of heat.
This is related to the idea that time arises from entropy increasing, but is more nuanced.
The sense in which time gets cast in this analysis consists of the timeline, and the flow of time from past to future.
Timing does not play a role. The idea that breakfast is a time for those who eat it doesn't occur.
Timing may not depend on heat for its general application. Instead, our sense of time might come from brain mechanisms as described here.
Another interesting group of people live on the island of Sommarøy in northern Norway.
They petitioned the government to establish a "Sommarøy time-free zone",
where there are no clocks, no listing of when activities start and stop.
People would be free to do things whenever they felt like it. This would be an example of how time can be thought of as internal to processes.
In fact, it was a marketing campaign to increase tourism. But many people really liked the idea.
A key concept since the early 20th century is spacetime, the topological (and generally metric,
meaning having measures like meters and seconds) space supposedly underlying everything.
Einstein argued successfully that the way to understand gravity is to view it as distorting spacetime.
This might sound familiar, as direction selective receptive fields are analogous distortions of space and time.
Distorting a straightforward separable receptive field into an oriented, inseparable version of space and time changes the way neurons respond to moving stimuli,
just as a black hole warping spacetime changes the way light moves around it.
And spacetime is nothing other than gravity, just as a spacetime receptive field is nothing other than a neuron's response properties.
The universe is not homogeneous, so that gravitational fields vary greatly across space.
Recent theoretical physics that took this fact into account as well as the fact mentioned above that time depends on gravity,
have posited novel predictions of how different parts of the universe have expanded
(Timescape cosmology).
Physics in the 21st century is challenging a lot of the fundamental delusions we have about space and time.
An explanation of how space is a delusion is given by Lee Smolin .
He frames the issue in terms of how causality depends on proximity, and that at the quantum level some events are linked causally even though they are far apart.
This explains the violation of locality seen in entanglement, where two particles can depend on each other's properties despite being far apart.
Our experience does not include many of the behaviors studied by physicists, so it's no surprise that we're deluded about how space and time are not what they seem.
From the point of view of biology, many of these physical questions don't matter much.
We can be easily deluded about quantum effects at small scales that we don't experience.
What counts is what we experience, which is what matters to the brain.
Biology and geology, what is commonly called evolution, are based on how things change in time.
But we don't directly experience the evolution of stars, unless they are popular musicians.
Neuroscientists are continually finding ways that our brains fool us into believing delusions.
Our reality is not what it seems, indeed, because it is created by brain processes arising out of mechanisms to improve survival,
rather than to provide us with a copy of the outside world. Our realities are created by the interactions between our brains and the outside world.
A recurring question is when did time begin? The usual answer is that time began at the Big Bang.
The universe may have been vanishingly small, perhaps only a Planck volume, but expanded dramatically.
This expansion had several phases, but they occurred within 10-36 seconds, ten million Planck times.
Since time had begun only that long ago, the time disk only had periods less than that.
In terms of frequency, the reciprocal of period, only enormously high frequencies were present.
Thus, anything that was present changed rather quickly.
Space was one of those things that was present, and it expanded at a predictably enormous rate.
If one fails to appreciate that time consists of frequencies and phases, recognizing these interactions becomes more difficult.
20 As mentioned a couple paragraphs down, Einstein believed the universe was static, and had poor intuition about quantum theory.
Physicist Philip Anderson had a brilliant career in which he used his finely honed intuition to see solutions to problems in many domains.
However, when he started working on high-temperature superconductivity, he stumbled because his intuition was not correct.
See A. Zangwill, A Mind over Matter: Philip Anderson and the Physics of the Very Many, Oxford Univeristy Press, 2021.
Hubel and Wiesel were amazingly correct in their conclusions based on their original research on the visual system that encompassed hundreds of hours recording from single neurons, but, as described above,
did not appreciate that direction selectivity depends on timing.↩
A subject of continuous interest is "the arrow of time".
Why does time appear to proceed in one direction, so that we are unable to go "backward" in time? We remember the past but not the future.
Physically, some argue that there is no basis for this asymmetry.
And, as discussed above, time may not exist physically. Many people have argued that time is an illusion.
That suggests that it is created by our brains, the source of all of our illusions, delusions, beliefs, errors, as well as any sorts of truths we might run across.
A common argument to explain why time is directed involves entropy. In particular, the second law of thermodynamics states that,
over time, entropy can not decrease in an isolated system. That is, time has a direction because a physical quantity changes in a certain direction over time, namely entropy increases.
Entropy is a technical term that is often defined as disorder.21
The idea is consistent with our common experience that things tend to fall apart, get messier, increase in complexity, and change in many other ways over time.
One expression of the second law is that heat does not move from a cold place to a hot place, whereas it does go in the reverse direction.
If you put ice in a hot drink, it doesn't make the drink hotter.
Muller provides an excellent discussion of why entropy does not explain the arrow of time.
Eddington proposed the idea in 1928, but his argument was simply that the two quantities, entropy and time, were related by sharing an apparent direction.
No quantitative or other sorts of evidence has ever been provided for entropy's causative role in the arrow of time.
In fact, as Muller illuminates, our more typical experience is that entropy decreases over time.
Locally, the activity that we experience tends to increase order, although that takes energy that gives off heat into the vast universe.
We aren't normally aware that the universe is getting hotter and its entropy is increasing, however.
Let's say that you ask somebody to write something on a blank piece of paper. You don't know what they're going to write.
Once they've written it, you can read what they wrote, and you then have information you didn't have before: entropy has decreased.
Our experience commonly consists of learning things, knowing more over time. Our brains tend toward decreased entropy over time, at least until our brain structure and function decay. It would be of interest to test whether the sense of the direction of time is related to brain entropy.
When memory function is disrupted, does time change? We noted above one example of time reversal in visual perception. There are many other situations in which an animal's view of time can be altered.
Another way that time might acquire a direction could be based on the fact that the universe is expanding. How that might give us a sense that time has a direction is unclear, since we only recently were able to "see" this expansion.
Poincaré makes the important point that motion is always relative. We don't realize that we are moving unless we observe something else that does not move along with us at the same direction and speed. So if time moves, what does it move with respect to?
Causality defines an arrow of time, in that when one thing affects another thing, the cause must precede the effect in time. If your mother gave birth to you, one can conclude that she was born at an earlier point in time than your birth.
Time and causality are more equivalent concepts than explanatory, but could be the basis of time's direction. As mentioned above, when the direction of causality between two processes is unknown, looking at the sign of the latency of their correlation can determine which preceded the other.
The two dimensions of time, frequency and phase, differ in their relation to the direction of time. Frequency does not participate directly in direction. Phase alone determines the direction of time. If phase does not change, the direction of time does not change.
If phase changes by a full cycle, time does not change, a full cycle being the same as zero cycles. But recall that if phase changes by a half-cycle, time does not have a directional change either: one could say that it has two directions, but the point of time having a direction is that one direction is favored over the other.
The direction of time must arise because of phase changes that lie between zero and half-cycles. Temporal phase commonly changes by small amounts, and changes consistently in its direction around the cycles, although it can reverse this direction.
Those reversals obviously do not contribute to our sense that time is directed. Only when phase changes in an expected manner do we relate those changes to the flow of time, as with an apple falling down, rather than up.
This is sensed by the multitude of direction selective cells that exist asymmetrically, with many more cells for one direction than its opposite.22 So the direction of time may be equivalent to biases in our direction selective neuronal populations.
A commentary on Hasson et al. (2008) also makes this point. Their Figure 1 provides a simple toy example of how our brains respond differently to the two directions of time.
We presumably have more neurons that respond to a cat falling down than to the same cat falling up.
The frequency dimension is nonetheless important, on the other hand. Different processes occur over different time scales. Slow changes in time, over years for example, do not depend on neurons that respond over much shorter time scales.
Only those neurons that are direction selective over periods on the order of years provide the sense of these slow changes. During a year, we might work on a project that gradually gets closer to completion. During that year, the project can have setbacks that move it away from completion.
Our sense of the direction of time over longer time scales depends only on the low frequency activity, ignoring the higher frequencies. And of course the direction of time over shorter time spans is dominated by those higher frequency neurons.
We normally distinguish between spatial and temporal dimensions based on the directionality of time.
We think of time as having a direction, but space is bidirectional (or hexadirectional).
But when we think that objects fall down, is that because time has the direction in which things fall, or because things fall down, in one spatial direction?
We can trade directionality between time and space. Barbour discusses this in terms of a simple physical model, a stack of spaces, a sandwich model that can be sliced in any spacetime direction.
The space-time plot in Figure 45 shows this tradeoff as well.
The correct view is that direction is a property of space AND time, or more generally whatever process is of interest AND time.
It should be clear that time does not really move at a single speed, as is typically implied by the one-dimensional model.
Time moves at all speeds, slowly for experiences that unfold slowly, and faster for briefer experiences.
Many of our experiences have components at a range of frequencies, and the different rates at which time changes disperse.
Our brains do not typically get confused by this, but instead parcel out time into a set of frequency bands within which dispersion is smaller.
We have an idea of duration, presumably corresponding to how neuronal activity changes at different low temporal frequencies. Single neurons are tuned to different frequencies, and could potentially signal how long a process has been taking.
No counters are needed, duration might just be a property of this temporal frequency tuning. Neurons tuned to lower frequencies, like lagged cells and the amygdala neuron shown in Fig. 12, might be crucial for our abilities to maintain behaviors over long periods.
Transient nonlagged neurons tuned to higher frequencies permit behaviors that are more immediate over short durations. But transient neurons tuned to lower frequencies enable us to prepare for the future, in a predictive sense.
Kulashekhar et al. 2021 (also see Protopapa et al 2019) examined duration perception in the context of hierarchical processing,
and provided evidence that occipital (back of the brain) cortical areas tended to be active for shorter duration processing and frontal areas for longer durations. Hasson et al. 2008 similarly found a frontal bias for slower perceptions.
Note that long duration, low temporal frequency neurons tend to have longer latencies, so latencies could increase up a hierarchy in this sense.
But it is not the hierarchy that produces the longer latencies because of axonal delays; instead, it is a matter of needing to respond appropriately to extended processes.
The anatomic correlation with duration might reflect the temporal globalization that we experience:
our brains generally do local processing that is then stitched together into processing of longer durations.
Barbour defines duration in terms of ephemeris time, which depends on the motions of celestial bodies in the universe. In particular, it does not depend on a notion of time, but instead on physical quantities: energy, masses and distances.
This provides key information that time is not a fundamental quantity. However, it ignores that we have a biological sense of time that might perhaps be somewhat unlikely to depend on ephemeris time. 😉
The clock reaction consists of mixing some chemicals together, and finding that the solution turns to a different color. That process happens over time, and has a direction. That is the direction of time. The direction of time is the direction in which things change. Our brains go to great lengths to detect and generate the direction in which things change, the direction of time.
21 Entropy is defined in terms of probability, and is related to how many possibilities exist. More possibilities means higher entropy.
As the possibilities are narrowed down, the entropy is lower.↩
22 The sheaf of morphisms would be biased to rotations in one direction in temporal phase.↩
Time is everywhere, and obviously in music. Arts such as dance are also obviously dependent on timing.
The usual listing of the components of music include pitch, timbre, texture, melody, harmony, dynamics, form, tempo, meter, and rhythm. The last three clearly involve time. But the others do as well.
Sounds are carried by vibrations, typically of air, that modulate specialized neurons called hair cells in the cochlea. Pitch is related to the frequencies of those vibrations.
Vibration frequencies are mapped along the cochlea, so auditory frequency is turned into a spatial dimension.
Humans can hear frequencies between about 20 Hz and 20000 Hz, though with aging the high frequencies are no longer heard.
Pitch is NOT the same as sound frequency, however. Pitch is a perceptual concept, rather than a physical entity.
We hear the same pitch for various sounds. A sound where all but 440 Hz are present has the pitch of A 440 (the missing fundamental).
Fundamental with harmonics
Delete fundamental
Noise
Delete fundamental
In the first examples with the harmonic series (440, 880, 1320, 1760, ... Hz), one can argue that the missing fundamental is actually present, in the beats. The beats are produced by a nonlinearity that is present in many systems.
For instance, a squaring function has outputs at frequencies that are the differences between the frequencies in the inputs. So the overtone at 3 times the fundamental frequency (1320 Hz) and twice the fundamental frequency (880 Hz) subtract to get the fundamental (440 Hz).
In the noise example, however, there are no beats (or there are beats at every frequency, so more noise). So the nonlinearities that produce beating are not just in the sounds that reach the cochlea, but are also produced in the brain.
There are numerous different sounds that are matched in pitch. This is analogous to color, which is a perceptual quality related to wavelengths of light, but many combinations of wavelengths are seen as color matches.
Pitches are defined by phases across the period of an octave. In Western music, there are 12 pitches: A, A♯, B, C, C♯, D, D♯, E, F, F♯, G, and G♯. These pitches are repeated over many octaves.
Going from C in one octave to C in the next octave doubles the frequency, so the pitches are closely related (the higher C is the second harmonic of the lower C, and is often a component of the sound we call the lower C).
The phase difference between two notes is termed the interval. From C to G is an interval of a fifth, with the frequency of the G in the next octave up being 3 times the frequency of the C. From C to F♯ is half an octave, so a phase of a half cycle: the interval from F♯ to the next C is another half octave.
We encountered this interval above when discussing the tritone paradox, where phase differences of a half-cycle/tritone don't define a direction of pitch change. A given interval sounds the same in certain respects wherever it starts, so C to G and D to A are both intervals of a fifth, and resemble each other.
Just as we can eat breakfast starting at different times and they resemble each other, playing the same intervals starting on different notes (that is, in different keys) produces similar melodies.23
Timbre means the tonal qualities of sound, which are largely derived from those combinations of frequencies. We can learn to identify instruments and voices by the differences in their timbres.
For example, wind instruments with cylindrical bores, like clarinets, flutes, recorders, trumpets and trombones, produce overtones that are odd multiples of the fundamental. Conical bores, as in oboes, bassoons, cornets, saxophones, tubas, euphoniums, conch shells, French horns, and alphorns have both even and odd overtones (Movie 17).
Vocalists learn to control their overtones, and Tuvan throat singers exemplify what can be done by producing interesting overtones.
Sound texture is usually described in terms that don't explicitly depend on time. Usually the number of voices is emphasized: homophony, polyphony, monophony, heterophony. For me this is another example of a bias against the primacy of time.
All of the other components of music make up the substrate of texture: whether few or many pitches are employed, whether differing timbres are heard, how elaborately melodic elements occur,
the thickness of the harmonies, the dynamic range, the complexity of the forms, variety of tempi, metrical changes and oddities, and the intricacies of the rhythmic approaches. These textural elements can occur synchronously but are typically shifted over time.
Polymetric music is synchronous and asynchronous at the same time, so to speak! A fugue has notably rich textures because of the counterpoint, simultaneous melodies. Listen and watch this visualization of a fugue (Movie 18), noting how it depends on temporal phase.
Harmony is viewed as the vertical dimension of music, as opposed to melody being horizontal. Vertical refers to synchrony, but harmonies change over time predominantly. Chord sequences are the horizontal dimension of harmonies in many types of music.
Popular songs are known by their chord changes, so that blues changes (based on I, IV, and V, tonic, fourth, and dominant chords) form a category of songs.
Rhythm changes, derived from "I Got Rhythm" by George Gershwin, use I-vi-ii-V chords.
Musicians compose a wide range of melodies that follow a single set of changes, often known as contrafacts. A list of many of these is at List_of_jazz_contrafacts.
A good example is Charlie Parker's "Koko", a contrafact on the chord changes of "Cherokee",
played at a terrifically fast tempo with enormous virtuosity.
Many pieces of music have a tonal center, given by the key signature. That tonal center can change during the piece, however, via a modulation to a new key.
Modulations have directions. Sometimes they move downwards or upwards in pitch. Often they move between minor and major modes in either direction.
Other aspects of harmony can change during a piece, such as modes, extensions, resolutions, and voicings.
In many forms of music, the harmonic sequences resolve. A dramatic tone is produced by invoking tension with less euphonic harmony that resolves to something more euphonic and reassuring.
A typical set of chord changes that resolves is a minor chord followed by a cadence on the fifth degree, resolving to the tonic.
When a phrase does not resolve, the tension remains, providing the listener the sense of things to come over time.
Music is usually not symmetric over time: playing a melody or a chord sequence or a rhythm in reverse order gives a different experience.
One of the common manipulations in serial music is to do these sorts of reversals, for instance playing a melody followed by playing it in the reverse, "retrograde" direction.
The intervals between consecutive pitches might also be reversed ("inverted") in pitch space.
Dynamics, the loudness of musical sounds, depend completely on time. Musicians use dynamics to express emotions and to draw pictures. Ravel's Bolero increases monotonically in volume and textural density throughout its duration, parallel to the Michael Snow film discussed below.
Amplification became important in order to provide greater dynamic ranges to certain instruments that can't sound loud acoustically. Usually, music has crescendi and decrescendi passages where loudness increases and decreases.
There are also accents on certain beats that emphasize parts of the rhythmic and melodic structures.
The form of a piece of music comprises longer durations. For example, a popular song might have a chorus of 32 bars, with the first, second and fourth sets of 8 bars having roughly the same structure, and the third set varying that structure.
This is an AABA form, with the B section sometimes called the bridge. Typically, the chorus is repeated, often twice at the beginning of the performance and once or twice at the end.
Sonata form has three main parts: exposition, development, and recapitulation. This form became so popular during the 19th century that it developed numerous variations. The main idea is that a theme (or set of themes) is presented, developed by changing aspects of it, followed by coming back to the original theme.
This form usually depends on modulations of the tonal center, timbral, rhythmic and harmonic variations, and different textural presentations.
The elements of form most often have durations of many seconds. How does the brain know where it lies in the form? Neurons that are sensitive to these elements might be active over many seconds. However, it is possible that neurons are active at different phases of the more extended elements as well as being specific to those elements.
Another obvious temporal component of music is tempo. Tempi can be denoted in terms of how many beats (e.g., quarter notes) should be played per minute. This is clearly a frequency. However, it is important to keep in mind that the primary element of timing is phase.
A piece of music is often performed at different tempi, with the elements occurring at the same phase each time, but at different times on the timeline. When learning a piece of music, it is common to slow down the tempo so that one can find the notes more easily.
That does not interfere with future performance because what counts is phase, not the points on the timeline where notes occur.
Meter refers to how many beats occur in each measure, where the music has been divided into a series of units (measures) that are assembled into larger units (e.g., phrases, choruses, movements). This concept is derived from early poetry. In ancient Greece, an important metrical structure was Epic Hexameter.
This probably originated in oral traditions for singing the stories that are now associated with Homer. When analyzing the Iliad and Odyssey, each line is divided into six feet, and each foot has 2 or 3 syllables, with the stress varying slightly across those syllables.
Not only the metrical structure, but also the structure of the phrases in epic poetry is characterized by parataxis, the use of shorter phrases without subjunctive clauses. Analogous structures appear in music.
I don't know much about tala, an analog of Western music's meter for Indian classical music. It is a more flexible construct, sometimes carrying information about longer sequences of notes. It depends less on accented beats, though a variety of accents are used.
It can be altered by the improvising performer. That is, a tala opens the musician to creative expressions in time.
As in Western music, the tempo can be varied: the tala is a matter of phase (Movie 19).
Finally, we can hardly dissociate rhythm and time. Cardiac rhythms, walking rhythms, working rhythms, daily rhythms, monthly rhythms, seasonal rhythms, and the rhythms of our lifespans have all been reflected in musical compositions. Inversely, musical rhythms affect our physiological rhythms.
We change our musical preferences over the various phases of our lives. And music changes dramatically over a typical human lifespan.
Rhythm is mostly about timing (as opposed to duration, for example). Although a simple rhythm might consist of a series of beats at different phases of a cycle, more complex rhythms involve multiple individual rhythms superimposed over one of more cycles.
A trained percussionist can play a trap drum set (a collection of drums and cymbals and other devices) with two hands and two feet, creating four distinct rhythms, "four limb independence". This is an extension of the exercise where you pat your head and rub your tummy.
One hand is playing beats on a drum while the other is hitting a cymbal at different times, one foot hitting the bass drum for emphatic beats and the other foot driving the high-hat cymbal in its own patterns.
These sorts of polyrhythms are typical of certain composers. Elliot Carter used them extensively. So did Don Vliet (Captain Beefheart).
Ba'aka music, as well as much of West African music, is fundamentally polyrhythmic.
Scriabin, Brahms, Boulez,
Stravinsky, Ligeti,
Reich (note that the shift is a latency difference between the two parts),
Jo Jones and Max Roach on Booker Little's Cliff Walk,
and many others used numerous varieties of multiple rhythms overlapping. Drum circles generally involve many players interacting with distinct patterns that create a complex groove.
Music presents these elements in orders that are highly structured in time. Serial music plays with these ordering concepts, for example by playing a twelve-tone row forwards and backwards.
Pierre Boulez serialized aspects of music beyond pitch, ordering dynamics, durations, attacks (the approaches to sounding notes), and timbre. Ordering in time elsewhere in music is based on gradual, consistent changes that are described by phase values at low frequencies.
Composer Karlheinz Stockhausen wrote a thesis he called "How time passes by" in which he details the structures involved in serialization, with reference especially to his composition Zeitmasse (Time-measures).
He refers to phase repeatedly, but in an idiosyncratic usage.
Finally, here is an account of listening to music by somebody who could not hear, Helen Keller:
Last night, when the family was listening to your wonderful rendering of the immortal symphony someone suggested that I put my hand on the receiver and see if I could get any of the vibrations.
He unscrewed the cap, and I lightly touched the sensitive diaphragm. What was my amazement to discover that I could feel, not only the vibration, but also the impassioned rhythm, the throb and the urge of the music!
The intertwined and intermingling vibrations from different instruments enchanted me. I could actually distinguish the cornets, the roil of the drums, deep-toned violas and violins singing in exquisite unison.
How the lovely speech of the violins flowed and plowed over the deepest tones of the other instruments!
When the human voices leaped up thrilling from the surge of harmony, I recognized them instantly as voices more ecstatic, upcurving swift and flame-like, until my heart almost stood still. The women's voices seemed an embodiment of all the angelic voices rushing in a harmonious flood of beautiful and inspiring sound.
The great chorus throbbed against my fingers with poignant pause and flow. Then all the instruments and voices together burst forth — an ocean of heavenly vibration — and died away like winds when the atom is spent, ending in a delicate shower of sweet notes.
Of course this was not "hearing," but I do know that the tones and harmonies conveyed to me moods of great beauty and majesty. I also sense, or thought I did, the tender sounds of nature that sing into my hand-swaying reeds and winds and the murmur of streams. I have never been so enraptured before by a multitude of tone-vibrations.
As I listened, with darkness and melody, shadow and sound filling all the room, I could not help remembering that the great composer who poured forth such a flood of sweetness into the world was deaf like myself.
I marveled at the power of his quenchless spirit by which out of his pain he wrought such joy for others — and there I sat, feeling with my hand the magnificent symphony which broke like a sea upon the silent shores of his soul and mine."
The Auricle, Vol. II, No. 6, March 1924. American Foundation for the Blind, Helen Keller Archives.
23 I'm ignoring here that most music deviates from the simple ratios of pitches described.
The scale is usually tempered, so a form of just intonation is the primary way of tuning instruments.↩
Film consists of visual imagery that is extended in time. Speech, music, and story telling add to the visual base. The elements of music discussed above have analogues in film. Rhythmic cutting, harmonic cinematography, and visual textures make up key aspects of film.
It can help to appreciate how important temporal processing is for watching a film by recutting a film into an entirely different order. "Of Oz The Wizard" provides an excellent tour-de-force example.
Matt Bucy recut the well-known 1939 film based on alphabetical ordering, primarily of each word spoken (or barked by Toto). So it begins with all of the frames after the word "a" is spoken (there are many) until another word is heard. Comprehension is sacrificed, but the rhythm is fascinating.
Uri Hasson had subjects watch movies that had been recut with various scramblings, including running backwards, of the order of segments while imaging their brain activity.
Early visual areas were activated by brief segments even when scrambled, but other areas cared about the order, as expected by our experience of trying to follow Bucy's film.
Hasson and colleagues ventured into connecting neuroscience and film studies.
Besides those kinds of dependence on phase, temporal frequency comes across as a key aspect of film. People often comment on the blistering pace of certain films.
At the opposite extreme are films like Ozu's, where relatively little drama occurs (Movie 21).
Michael Snow's film Wavelength (Movie 22) consists of a zoom over a 45-minute duration with related changes in picture and sound.
Andy Warhol made several films where nothing happens for many hours (e.g., Empire (Movie 23), more than 8 hours of the Empire State Building, intended "to see time go by").
Filmmaker Masahiro Shinoda talked about Kenji Mizoguchi's film "Ugetsu" in a long interview. He saw Mizoguchi as using "human time" and "historical time". This might be similar to what I argue here,
that biological time is related to our activities, as opposed to clock time.
Hollis Frampton made my favorite example of how film uses time. A mathematical proposition called Zorn's Lemma examines an object called a partial order. A partial order is a relation where elements can be ranked as in a total order, but some pairs of elements can not be ranked that way.
It is almost always depicted as a tree, with branches extending upwards. Two elements on the same branch can be ordered, but elements on separate branches can not. This is a spatial realization of the relation. Frampton's film "Zorns Lemma" (Movie 27; reading the linked article's Production section might be illuminating) instead bases the partial order on time.
He takes the letters in the Roman alphabet (put into 24 classes by interchanging I and J, and U and V), and displays them, usually in a shot of a sign, for one second at a time, running through the 24 letters before cycling back. Eventually each letter is replaced by a non-alphabetic image, representing the top of that branch.
What the mathematical Zorn's Lemma states is that in any partially ordered set where each branch is entirely below some height, the entire tree is below some height. That sounds completely reasonable, as if it must be true.
However, the statement is taken to apply to infinite as well as finite sets, and those might not satisfy the statement (since an infinite series of finite values can be infinite, like the whole numbers).
In fact, Zorn's Lemma can not be proven based on the axioms of Set Theory. However, it can be proven if one also assumes the Axiom of Choice or equivalent statements that aren't provable by Set Theory.
The Axiom of Choice says that given a collection of non-empty sets, one can form a new set containing one element from each of the original sets.
Sounds reasonable, but hard to say for infinite sets.
Frampton substituted time for the usual spatial dimension in which partial orders are presented.
Frampton's manipulations in time could have been done by panning across space, but he went to great lengths to construct a phase-based view of time, "the illusion of space or substance", that resonates with what I've described in this book.
Varying the rate at which frames of a film are captured vs. projected permits slow- or fast-motion. Stan Brakhage filmed towels falling down in slow motion to make money in a fabric softener commercial.
Another of his commercial films was a collaboration with the ingenious physicist/author George Gamow (inventor of the Big Bang), "Mr. Tompkins Inside Himself". I haven't found a way to view that film, but another Gamow film (without Brakhage) is "Mr. Tompkins in Wonderland" (Movie 28).
That film lacks Brakhage's artistic touch, but explores many of the physical and cinematic concepts we have discussed here.
24 We may perceive rapid visual motion by doing something more like comparison across frames.↩
Finally, I want to point out some philosophical ideas that readers might want to take into account when thinking about this book.
The primary argument here is that thinking of time in terms of phase and frequency is somehow better than thinking in terms of points on a line.
I could refine what is meant by better, and hopefully have suggested ways that phase and frequency are more useful.
But the larger point is that such arguments are misplaced.
If one person asks another what is the best film, and the second person answers "Casablanca", and then the first person immediately says no,
it's "Citizen Kane", what is going on? For one, it is not likely that films can be ranked in a total order.
They might not even fit into a partial order. Beyond that, should the first person say "no, that answer is wrong"?
I would suggest, and expect that everybody knows this, that the questioner might consider what the answer is based on before objecting to it.
It should be clear that this is a subjective judgment, meaning that it comes out of the experience of the speaker.
The two people in this argument, and any two people you could pick, have quite different experiences.
These different priors/beliefs/mindsets, or whatever you prefer to call it, cause them to make different judgments.
Arguments about less subjective topics, like time perhaps, are similarly based on priors.
I have attempted to add some evidence to justify my beliefs in this book. But I respect that others have different priors and don't think the same way.
I also argued that we should challenge our beliefs with evidence and reasoning.
We learned a lot of dogmas that can lead us astray. Common wisdom can be wrong.
But that last statement should be taken with the caveat that right and wrong are not appropriate ways of thinking in most cases.
Instead, we should consider under what circumstances, what priors, does a statement seem right or wrong.
It may be that the timeline is more useful in many contexts than the ones dealt with here.
Just as perception of sensory signals depends on context, ideas work in some places and not in others.
Lighting a match can be useful to light a candle, but not where more flammable materials are nearby.
But do let me know where I'm wrong, please.
All life is made out of cells. These are little bags of sea water, with a vast variety of specializations. One large class of cells that exist in animals is neurons.
Neurons have a cell body like all cells, but usually have special processes that are often placed into two groups: dendrites and axons.
One neuron often projects to other neurons, typically by having its axon contact dendrites.
The makeup of the salt water inside and outside of cells, and the permeability of the cell membrane to different ions in that makeup,
creates a membrane voltage that is negative inside relative to outside of the cell.
A typical voltage is -70 mV (millivolts). We say that cells are polarized, more negative inside. If the voltage becomes less negative, we say that the neuron is depolarized.
If the voltage becomes more negative, it is hyperpolarized.
Those changes in voltage constitute the main signals in the brain. A specialization in many neurons is a type of sodium channel, a protein that permits sodium ions to pass into the cell.
These particular sodium channels are sensitive to the voltage across the nearby membrane. When the membrane potential gets depolarized, the channels become more permeable to sodium.
That permits a sodium current to pass, driven by the imbalance in sodium ions, far more outside the cell than inside.
These positively charged sodium ions induce a positive current that further depolarizes the cell.
A positive feedback loop thus very quickly changes the membrane voltage, until the neuron's polarity is reversed so that the inside is more positive than the outside.
The baseline is quickly restored as the sodium channels become impermeable to sodium, and because potassium channels become more permeable and the imbalance in positively charged potassium ions (more inside) repolarizes the membrane back to -70 mV or so.
The process described in the last paragraph was described by Hodgkin and Huxley in 1952. The rapid changes in voltage in neurons are called "action potentials", also commonly called spikes.
The entire process of depolarization and repolarization lasts a millisecond or two. Spikes that are generated in the cell body can propagate down the cell's axon.
At the axon terminals the spikes cause release of molecules called neurotransmitters.
Signals are conveyed between neurons mainly by releasing neurotransmitters from the axon and having those molecules bind to proteins on the dendrites of other cells, causing changes in the voltage across the membrane of the dendrite.
Neuronal activity consists of series of many spikes emitted over time. In sensory physiology, experiments often apply stimuli and measure the responses of single neurons to those stimuli.
Those responses have been measured mostly by inserting an electrode into the brain. The electrode picks up the voltage changes that spikes generate in the fluid near the cell.
Allen Humphrey found that he could consistently record from the small lagged cells in the lateral geniculate nucleus (LGN) with electrodes pulled from glass tubes
modified in a microelectrode puller by heating and melting the glass in a controlled manner,
then pulled apart to create a fine tip. When he filled the micropipette with a solution of 3 M KCl (a relatively high concentration of potassium chloride),
he never recorded from a lagged cell. When he instead used a 0.2 M KCl solution, he recorded from many lagged cells.
The lower concentration results in a higher impedance (resistance) that means that neurons need to be close to the tip to be recorded.
We confirmed this by first using a 3 M KCl electrode to find the LGN, because those electrodes pick up cells easily.
This was followed by using the 0.2 M KCl electrodes to record from both large and small cells, with many of the small cells turning out to have lagged responses.
Peristimulus time histograms (PSTHs) are used to display the results. These are generally averages of the responses over several repeated trials.
A stimulus is presented, the times of the spikes relative to the stimulus timing are recorded, and a histogram is built up over the repetitions of the stimulus presentation to obtain an idea of how exactly the cell responds.
The visual pathway originates in the retina. The output of the retina consists of the axons of ganglion cells, which project to numerous parts of the brain.
One of the targets of the retinal ganglion cells is the lateral geniculate nucleus (LGN).
The LGN has several divisions and cell types, but the main structural feature is that many LGN neurons have a dominant input from a single retinal ganglion cell.
These LGN neurons relay the signal from the retina on to area V1 (first visual area) in cortex. Cortex is divided into 6 layers.
The input from subcortical regions like the LGN is primarily targeted to the middle layer IV, with different LGN cells targeting slightly different parts of layer IV and nearby layers (a substantial input is found in layer VI as well).
Connections within and between cortical layers provide the substrates for processing information, which is then passed on to cortical and subcortical regions.
Area V1 sends a massive input back to LGN, and feeds visual information to cortical areas V1, V3, V4, MT, and elsewhere (Fig. 2).
A function of time (or space) corresponds to another function of temporal (or spatial) frequency.
If we take a function f(t) in the time domain, it corresponds to a function F(ω) in the frequency domain, where ω is temporal frequency.
The frequency domain function is two-dimensional, often described as taking values in the complex plane.
The dimensions are amplitude, the distance from the origin in the complex plane, and phase, the direction from the origin in the complex plane.
So we can write F(ω) = A(ω) ⋅ e2πiφ(ω). The functions A(ω) and φ(ω) are the amplitude and phase components.
The complex exponential e2πiφ(ω) has values on the unit circle (the circle defined by the points lying at a distance of one unit from the origin) in the complex plane.
A phase of φ=0 gives a value of 1, a phase of φ=¼ gives a value of i=√-1, a value of φ=½ gives a value of -1, and a value of φ=¾ gives a value of -i=-√-1.
The conventional arrangement of the complex plane has 1 to the right, i upwards, -1 leftwards, and -i downwards.
Many interpretations of the mathematical objects like the complex plane exist. For our purposes, a function of temporal frequency changes amplitude across temporal frequencies.
Usually, amplitudes are small at low and high frequencies. That means that little responses are present for slow and fast changes.
Phase changes systematically with frequency, increasing with increasing frequency. The change is approximately linear.
Phase represents WHEN responses occur, so the linearly increasing phase with frequency means that responses occur later in the cycle as frequency increases.
This is obvious, because the length of a cycle decreases with increasing frequency. Responses only occur after some latency, and that latency is a greater portion of the cycle as frequency increases.
We have speculated that huge questions about emergent properties and the power of our brains might be posed in the context of the example of direction selectivity. Timing is key to that example, and we expect that would carry over in other domains.
An emergent property that is broadly familiar is childbirth. Living things produce more of their kind, and in the case of sexual reproduction, two individuals who have both commonalities and differences produce a new individual by combining themselves.
Generations of this process over millennia under evolutionary pressures create unimaginable novelty.
The numerous speculations above are not likely to be borne out by experiments. But perhaps some of them will be useful at stimulating thinking about time.
I wonder why more people don't appreciate the frequency domain. It may just be that it seems foreign, and I hope that the explanations here might make people more comfortable with it, since it seems so simple and provides so much more explanatory power.
As the late phases of this work approach, I have entered into the late phases of my life. A diagnosis of Primary Progressive Aphasia and Alzheimer's disease means that I am likely to lose language, among other things. I am quite curious about how that will feel, as language is one of the most compelling of our temporal faculties.
Will I continue to enjoy music and film, as well as emotional contact with my loved ones?
One of my all-time favorite books is Douglas Hofstadter's Le Ton beau de Marot: In Praise of the Music of Language.
I have had the experience of communicating with people without a common language, and am interested in how well I'll be able to do that.
Will my creativity decline? Will I still enjoy music? Lots to learn!
Interactions with people who influenced my thinking
I started my undergraduate work in Physics. I wanted to work with Murray Gell-Mann on particle physics.
The only time I saw him, however, was when I spotted him hunting mushrooms.
In high school, I had won $50 in a science fair for my presentation on A Hypothetical Mechanical Model of the Photon
(in 1971, that was a lot of money for me). It was not soundly based on Physics,
but was entertaining, partly by depending on an integral that nobody I asked could evaluate,
including brilliant friends like Andy Zangwill, David Sze, and Brad Osgood, as well as our teachers,
until somebody at Carnegie-Mellon University identified it as an elliptic integral.
The project hypothesized faster-than-light behavior. In college, one of the greatest physicists,
Richard Feynman, known at Caltech as God, did an occasional session with first and second year students.
One day I asked him about tachyons, particles that travel faster than light.
He quickly dismissed the notion of tachyons, citing the fact that they would emit Cerenkov radiation
and continuously speed up to infinite speeds (Steven Kenneth Kauffmann, Cerenkov Effects in Tachyon Theory, 1970).
He then went back to answering the sorts of questions he loved,
such as how sugar dissolves. My appreciation of that attitude took awhile.
My first year Physics advisor was George Zweig. He was a prodigy,
who obtained a faculty position when he was in his mid-20s.
He came up with the idea of quarks, unusual particles that are the building blocks of protons and neutrons,
independently of the guy in the next office, Gell-Mann, who got the credit
(Zweig called them "Aces"; Gell-Mann got the word quark from James Joyce' Finnegan's Wake).
By the time I knew Zweig, he had switched his research to Neuroscience, in particular auditory physiology.
He told me about that and gave me some fantastic reading, Georg von Békésy's studies on how the cochlea works.
I had no use for any domain other than Physics at the time, and Zweig's enthusiasm started to change my perspective.
Physics lasted through half of my second year, with my last course Feynman's class on Quantum Mechanics.
Robert Sharp was a huge influence on me,
through his excellent lectures and the trips we took to the Grand Canyon and Death Valley.
I went ahead of the group to the Canyon, hiking down Hermit Trail on my own before going with Professor Sharp the next day.
He pointed out the massive fossil bed near the top that I had completely missed.
He knew practically every rock in Death Valley, telling us what was around each bend.
Professor Sharp told stories about the discovery of seafloor spreading, how various unconformities emerged,
and how sand dunes stood and fell. Now there's a mountain on Mars with his name, an appropriate honor.
I spent much of my college years in the mountains and the desert, with numerous trips to the Canyon.
I often wished I could get a degree in Nature.
I had been exposed to Linguistics. The professor for this course, Bozena Henisz Dostert Thompson,
spent the first term in her home country of Poland, and her newlywed husband Fred Thompson took over the teaching.
Thompson had diverse training and interests, having studied with logician Alfred Tarski,
and worked in computer science. He developed natural language abilities in computers,
which at the time were not really capable compared to what we have now.
He taught us about Chomsky's theories of grammar,
and I did an independent study with him that I wanted to be about structuralism,
but he made it primarily a deep dive into Nominalism (Nelson Goodman and Willard Van Orman Quine).
I was slow to appreciate the good parts of Nominalism, but am now committed to avoiding categorization of people.
So I started to think Biology might have some worthwhile ideas.
That was reinforced by doing some experiments for the Psycholinguistics term,
in which I performed experiments with my biologist and soccer friend John Lehmann.
We borrowed a tachistoscope, a slide projector with a shutter, that can flash images very briefly,
from Dahlia and Eran Zaidel, who were working in Roger Sperry's lab.
Sperry had pioneered studies of the two hemispheres of the human brain,
thanks to observations on a set of patients who had their hemispheres separated surgically
to alleviate symptoms of epilepsy. John and I examined how stimuli were lateralized,
processed better on one side of the brain. John's stimuli worked far better than mine.
My best friend, Robert Tajima (Taj), helped me enormously to move further toward Biology.
I accompanied him to Sperry's course that ranged from planes of section (pure basic anatomy) to consciousness.
Even more revealing was the Neurophysiology course, two terms of which were taught primarily by Jack Pettigrew.
His thrilling lectures, talk sessions, and personal guidance were life-changing.
Jack was an Australian maverick. He was a free spirit, possessed the kind of one-in-a-billion intellect
that captivated any audience, and always overflowed with ideas. He didn't always chase down the evidence,
but in some cases worked quite hard to do so, in particular with his claim that big bats are primates.
His lab was decorated inside and out with art made by his wife Rona,
and both his lab and his home were populated with varied experimental animals.
His most memorable lecture was "Love is a plastic state,"
in which he argued that our brains become more susceptible to change when we're in love
(or on certain drugs or under other conditions).
Jack gave me a paper by William C. Hoffman about the "Lie algebra of visual perception"
that proved instrumental in seeing how mathematical ideas can be applied to neuroscience.
Although I didn't make the connection, Hoffman proposed a form of the idea I treat in this book, that sheaf theory applies to the brain.
Jack similarly gave me a wonderful paper by Max Cynader and David Regan
that proposed a simple arithmetic solution to how we determine whether a moving object is going to hit us in the head.
Jack suggested that Max might be a good person to work with. He was right.
Jack is known for many discoveries and theories.
He showed how neurons in visual cortex help to create stereopsis to let us see depth.
He proposed and tested a number of molecules that might regulate cortical plasticity.
By comparing visual mechanisms in different species,
he argued for convergent evolution that produces binocular vision with similar algorithms despite varying structures.
He famously campaigned for the idea that big bats are flying primates.
Jack took on projects involving baobab trees and rock art.
And he measured switching times for the bistable perception in binocular rivalry,
correlating those times with bipolar disease and schizophrenia.
Jack collaborated with dozens of other great minds, including the Dalai Lama.
He studied an equally broad collection of non-human creatures.
And his home was the whole world, despite his love for Queensland, Pasadena, Tasmania,
and the several other places he lived.
Taj and I also took Max Delbrück's course that covered a variety of biological and philosophical topics.
I got to know Max on annual trips to Joshua Tree, with his wife Manny and their children
(Tobi works on electronic chips that process visual stimuli,
including direction selective elements that analyze moving images;
Ludina Delbrück Sallam is an Arabic translator; there were two older children I didn't know),
Humanities professors David and Annette Smith's family, and several undergraduates.
Max kept star charts like the ancients.
My last year, he told me how his retinal detachments kept him from being able to make out the stars well enough
to continue this work, and asked if I'd take over his charts.
I stupidly declined, fearing I wouldn't do it justice.
Max viewed Science not as building a cathedral, but instead
people piling up stones
(also Beckett).
I found his attitudes refreshing and on point. Max deserved every honor possible, just a giant of a man.
David Smith gave me a special gift in bringing musician Charles Lloyd to campus on a series of Wednesday evenings
over a span of many months. Charles talked mostly about transcendental meditation and mucusless diet,
but did discuss music. He taught me many things from his expert perspective.
Notably, when I brought up Booker Little,
he immediately said "the greatest trumpet player who ever lived"
and proceeded to regale me about how Booker put him up when he first got to New York City,
and how they had been close friends from childhood. He asked us to bring in a record one week,
and I brought in Coltrane's Village Vanguard album. He proceeded to play the masterpiece Chasin' the Trane,
picking up the tone arm at the end and putting it back at the beginning 3 times.
Charles brought along his filmmaker friend Eric Sherman, who screened a series of great films by Frank Borzage,
Fritz Lang, Josef Sternberg, Kenji Mizoguchi, Orson Welles, John Ford, Peter Bogdanovich, and others.
This sparked my interest in film, which, along with music, has occupied much of my time since.
After college came two years in Central African Republic as a Peace Corps Volunteer.
Three months of training in MBaiki and Bangui gave me a start on speaking Sango, the National Language.
I learned how to fix my mobylette, kobé nguinza na gozo (eat manioc with manioc), and communicate with people without a common language.
Some of that training was provided by the incomparable Mokombo Antoine.
Halfway through training, we had a week to travel. I walked into the rain forest, hoping to see how the Ba'aka live.
The water filters had not been turned on at the agricultural university where we stayed, and everybody got sick that week.
I learned some Sango on my walk, but when I got to a tiny village, I asked for water as I was feeling terrible.
They didn't want to give me their rather dirty water, so they gave me mbako, manioc whiskey.
I tried to slake my thirst with the mbako, which was a bad idea. They fed me caterpillars that were delicious,
and put me to sleep in a tobacco-drying hut. I woke up at 3 am and wandered around trying to get some water,
checking all the leaves for any dew. Heading back to the university in the morning, I learned about everybody being sick.
After recovering, I went back out and made my way to Mongoumba, hoping to take the President's boat to Bangui.
The town's gendarme confronted me about what I was doing there. He was suspicious until I dug out a card we'd be given that said I was cooperant.
Suddenly we were best friends. He took me to his house, taught me to play kissoro, a stones in holes game.
He had his wife cook me the best meal I've ever had, wild mushrooms. After several days, I gave up on the President's boat and found rides to Bangui.
I lived up north in Ndélé for the rest of my time there, with a month back in Pittsburgh with my father,
who had suffered his fourth heart attack. He told me to go back to CAR, and he'd see me get my PhD,
an idea I hadn't ever considered. I hung out with lots of people who I never would have known otherwise.
My neighbors Jacques, Ali, and Malik, commerçant brothers, were wonderful friends and teachers.
A student, Lopère Jean-Nestor, became a close friend, along with his compatriots from the villages of Digba and Kottisako, who I referred to as the Ouadda Boys.
They often joined me for dinner, which was probably their only meal during the week.
They played music and sang, and we talked about all sorts of things out of school.
Amara, a musician who played the double reed keita, came to town from Tchad.
He could support himself because Ndélé had a Sultan with a court. Amara used circular breathing, had cheeks like Dizzy Gillespie, and a tremendously big sound.
We got to be friends, talking without a common language about music, and drinking douma, honey beer.
I had three pieces of technology with me: a Walkman cassette recorder, a Fuji Single-8 movie camera, and my Leblanc clarinet.
I recorded Amara and the Ouadda Boys and various other music on cassettes, and listened to a set of tapes I'd brought along.
I shot rolls of film that were sent by mail to Fuji and then to people I designated. Amazingly, I recovered every roll of film when I got back to the states.
I played the clarinet with Amara, but mostly sitting on the rocks above town. The Black Kites would swoop past, grazing my head.
When I returned from visiting my father, I got to work on a construction project that the Ambassador had funded, a new building at the school where I taught.
I borrowed a motorcycle and rode around Bangui putting together all the supplies we needed, and a truck to take them to Ndélé.
I rode with the truck, getting to be friends with the driver.
When we got to the Bangoran River 60 km south of Ndélé, the driver refused to cross, afraid his engine would flood.
I pleaded with him for a couple hours, then decided I would walk ahead, hoping that he would come along after the crazy white guy.
The plan worked. I knew that Digba and Kotissako were not far from the river, but he didn't. I bought the whole crew douma when we got to Kotissako.
A group of newly arrived construction volunteers arrived unexpectedly. I found them places to stay and hired another cook to help.
I had already hired locals to help with the demolition of the old building, and now the construction, and we got to work. I didn't deal well having other Americans around,
partly because most of them had no interest in the community. Another truck had come up without me to bring cement for our needed concrete work.
The cement wound up being stolen by the Préfét, David Zoumandé. I met with him regularly, and would ask him about the cement.
I finally got fed up with him, and told him explicitly that he had stolen the cement. He kicked me out of his office and told me not to come back.
That was fine with me, since I hated speaking French with him and didn't need him for anything.
That truck also left our load of reinforcing rods, rebar, at the other side of the Bangoran, which we later drove down to and walked across the river, at the end of Ramadan.
The Ambassador had also funded a project to bring water from a spring into the town.
I was in charge of the money for that project as well, but the work was supervised by the chef-de-genie-rural, a wonderful man named Thadée Ozzenguet.
We traded formboards and rebar, and became close and helpful to each other. Many years later, I corresponded with his son who was in Canada.
At the end of the rainy season, two more Americans arrived, Tony Nathe and Mark Rand, who stayed and taught for the next year.
The construction volunteers left, though two came back to replace the subroofing a little later.
We had great colleagues at the school, Eleguendo Joel, Yamtiga Albert, and others. Joel taught history,
and got up early every morning to listen to the news just in case a student asked about it. He fought the system, and had spent time in prison because of that.
I was a math teacher, but taught Biology and English as well, because faculty tended not to show up in distant Ndélé.
The school closed for a month in 1977 so that the students could practice marching in anticipation of the coronation of Bokassa I.
I also had a class kicked out of school for a term because they were misbehaving. Students had a difficult road for many reasons.
Most of them came from villages that were too hard to walk home to during the week, and they only really ate on weekends.
Some didn't have comfortable places to sleep at night. They were under tremendous pressure from family, townspeople, and teachers.
The girls had to deal with men soliciting them for sex, and the risk of getting pregnant.
There weren't books, only little notebooks they had to buy and copy into from the board.
The last thing I did in CAR was a trip to the most beautiful place in the world, Koumbala,
with the other teachers and the superintendent of primary schools, whose wife was the director of our school, and who had a car.
I bought a sheep, and we drove to Koumbala in his Land Rover with the sheep in the back.
At Koumbala, we walked to the top of the waterfall, slaughtered the sheep in the river, cleaned the tapeworms out of the intenstines, stuffed them with the organ meat,
and ate all the parts. I was a vegetarian, but tried everything and saw why people love the meat that most Americans never venture to eat.
After a wonderful weekend, we headed back, but ran out of gas a few kilometers before town. We walked the rest of the way.
When I got to Tony and Mark's house, Mark told me that my father had died. I sat and cried for hours.
Mark accompanied me on the trip to Bangui atop a truck. I didn't have many chances to say goodbye to friends, most notably Jean-Nestor.
After a long trip to Pittsburgh, I was quite ill, and my mother sent me to my father's doctor. It took another week to recover.
While in college, I pined to get away from academia and live away from cities. I succeeded in that by living in Ndélé.
Back in the states, I fell in love with the piece of woods we called Out Yonder, and bought it from my brother-in-law,
who had purchased it with money he got from doing a commercial for the Post Office. Peace Corps gives you a "readjustment allowance",
and I used it for the land. Otherwise I didn't need much money thanks to a pretty spartan lifestyle, and a teaching job at my cousin June Himelstein's alternative high school.
But eventually I ran out of money, and looked to get a job at the nearby West Virginia University. They paid me $3000/year to teach algebra and calculus, and I got a Master's degree.
I got sucked back into academia.
I was teaching calculus to engineering students at West Virginia University,
and noticed that a book had been left behind by the previous teacher. After class,
I went to return the book to that professor, but first scanned its content.
It was The Geometry of Biological Time, by Art Winfree, a beautiful book in every way.
I found the owner, Ken Showalter, in the Chemistry Department. Ken is a physical chemist,
and we wound up talking about the book and many other things.
At the time, Ken was working on a chemical reaction that involved the reagents sodium iodate and arsenous acid.
If you put these chemicals in a jar at the beginning of a lecture, they will sit as a transparent liquid.
At some point during the lecture, the fluid in the undisturbed beaker will suddenly turn black.
This is an example of a
clock reaction.
Inorganic chemicals can undergo reactions at regular or irregular times.
Ken had been looking at how the reaction in a tube of this solution can be triggered at one point in space,
creating a wave that traveled down the tube. We worked on analyzing these propagating waves.
I was living Out Yonder at the time, an hour's drive from Morgantown,
working in the woods, cooling off in the pond, then trying to figure out how the waves worked.
Ken and I sent notes (a few years later there would have been email) back and forth about our progress.
He was sorting out the chemistry, and I was playing with the math.
We each came up with the answers from our two perspectives at the same time.
I had seen that the waves could be described in a pretty (closed-form,
meaning easy to write down and read) function if the reaction was a cubic function of iodide concentration.
Ken had seen that the reaction was in fact a cubic. We nailed down how well the predictions fit the data,
determining the speed at which the waves traveled,
and published a paper with Adel Hanna.
That got me started on thinking about time.
I learned many things from Ken, especially about the wonders of collaboration.
Some people don't recognize that Science is about people. But humans are social animals,
and we thrive on our interactions.
The pleasure of doing Science is largely spending time with people you enjoy and appreciate.
Every once in a while you learn something, providing enormous pleasure.
This book will hopefully provide such pleasure, or at least be stimulating.
It has roots in Winfree's book, and steals its subtitle from his title.
I got to spend some time in June 1980 with Winfree in Salt Lake City at a meeting about Mathematical Biology.
We went up to the mountains, still covered by snow, and slid down on trash bags.
Winfree was driven by creativity. He liked to push the limits. Yet his work was accessible and applicable.
Carl Irwin made it possible for me to attend that meeting.
Carl was a math professor at WVU who for some reason took an interest in me despite my never taking a class from him.
He had earlier gotten me to a meeting in Philadelphia organized by Stephen Grossberg,
where I met George Sperling, Stuart Geman, and others who would reappear in my life.
Carl, and Paul Brown, a neurophysiologist at WVU in whose lab I worked,
taught me that helping other people without expectation of getting anything back is a prime goal.
Paying it forward is a beautiful philosophy. I have an expensive electric bike that Sohail Khan gave me,
saying "Pay it forward" and have learned that the point of life is to help other people.
Goro Kato spent a year at WVU as a visiting professor, and asked me who I was at a Math Department meeting.
Goro has an infectious, cheery personality. He got me studying abstract algebra again,
insisting on rigor that I have a hard time achieving. Our friendship persists,
and he has been my collaborator on the sheaf theory presented here,
though my poor understanding leaves the presentation here lacking.
The Math Department treated me well, and I enjoyed most of the course work, particularly Topology with Sam Nadler.
But I was more interested in Neurophysiology, and searched out somebody on the other campus to work with, finding Paul Brown.
Paul studied somatosensory processing in the spinal cord of cats. I participated in some experiments, but mostly came in at night to use his computer.
Paul had gone to an NIH-funded program to give computers to neurophysiologists. These computers were built by Ted Kehl, and used his BASIL language.
I ran the computer to simulate the development of kitten visual cortex, based on ideas I'd formulated thanks to Jack Pettigrew.
Paul was on sabbatical in Scotland much of the time, and we corresponded by mail about papers I was reading.
The training I received from Paul stands as one of the several large pillars I've stood upon. In his retirement,
Paul has written books and maintained online discussions about the end of life on earth.
I wound up at Brown University because it seemed relatively close to my Out Yonder land, and because I had met Stuart Geman and knew Jerry Daniels from Jack Pettigrew's lab.
My 4 years in Providence involved a lot of suffering around my lack of money and a lot of hard work, sometimes with difficult people.
But there were plenty of great times, including my eldest two daughters, listening to music with Phil Stallworth,
learning to think critically with Jim McIlwain, and especially knowing Philip Fiagbedzi and his wife Christina.
Philip got me through my comprehensive exams, although my Probability professor asked me about martingales, which I had missed learning about while at a Neuroscience meeting.
Jerry Daniels and Leon Cooper, my advisers, helped me through a lot of tough times, but also created them for me.
My graduate colleagues Paul Munro, Mike Paradiso, Mark Bear, Brad Seebach, Eugene Clothiaux, Doug Reilly, and Chris Scofield helped immensely to get me through my difficulties.
Mike Paradiso introduced me to Mike Shadlen,
who told me about spatiotemporal quadrature.
His son Josh Shadlen happens to have become a sheaf theorist, although Josh doubts its applicability to anything.
As my PhD program was coming to an end, I contacted Jenny Lund, an expert visual cortical anatomist,
who had just moved to Pittsburgh with her husband Ray, an equally expert developmental neuroscientist.
Jenny was enthusiastic about my coming to do a postdoc, but steered me to their new hire,
Allen Humphrey, who I knew from a job interview he had made at Brown.
We agreed that I would join them. However, at the vision meeting in Florida that year,
I ran into Max Cynader at the Myakka River state park.
I had applied to do my graduate work with him several years back
(but decided against it because I thought Nova Scotia was too far away from Out Yonder),
and he suggested I come to Halifax now as a postdoc.
So I wrote to Jenny and Al to decline their offer with regret,
mentioning that I would love to come work with them later.
In a very encouraging way, they asked me to postpone our plans until after I was done with Max.
Working with Max Cynader was a revelation about collaborations.
Max and I finished each other's sentences. We were quite similar in scientific temperament,
being fascinated with ideas. I continued to do experiments by myself, but got inspiration and support from Max.
He decided to move to Vancouver, so I had a highly productive year with him before going to Pittsburgh.
My work on adaptation aftereffects in single neurons had started in Providence,
but took off in Nova Scotia. I got to look at temporal processing.
During my time at Dalhousie, Al Humphrey suggested that I write a grant to fund my postdoctoral work with him.
Al and Rosalyn Weller had done experiments in Murray Sherman's lab in Stony Brook,
looking at cat lateral geniculate neurons by filling their axons with the enzyme horseradish peroxidase (HRP)
and visualizing the cell bodies, later progressing to experiments where they filled the cell bodies directly.
They became interested in cells reported by David Mastronarde,
and Al sent me Mastronarde's and their yet unpublished manuscripts on lagged cells.
I wondered whether lagged and nonlagged cells might be in spatiotemporal quadrature,
and wrote a draft of the grant that proposed to examine that question
and whether they might have something to do with cortical direction selectivity.
Al rewrote the grant almost completely to focus on the experiments he had been doing.
That was wise, because we were awarded the funding. When I got to Pittsburgh,
Al gave me Peter Bishop's papers to read, and we started trying to fill cells with HRP
after initial extracellular recordings of their visual responses.
The anatomical work went very slowly, only recovering a few cells in a year.
Meanwhile, the receptive field recordings went beautifully,
and soon I could see that lagged and nonlagged cells were in quadrature.
We published the LGN study in 1990, after sending a draft of the manuscript to Murray Sherman.
Sherman was critical, but did not keep us from publishing. Subsequently, he tried to sabotage our work.
He and Dan Ulrich put out a short paper arguing that lagged cells were an epiphenomenon of anesthesia.
Paul Heggelund and Espen Hartveit, who had been recording from lagged cells as well,
along with Al and me, responded with evidence that refuted Sherman's claims.
But Sherman was influential in making people skeptical of our findings.
This is despite how clearly Mastronarde had initially laid out the story,
and the replications by Heggelund and Hartveit and ourselves. The business of Science, of course, is a social sport.
I was anxious to get back to recording in visual cortex, and that work soon proved fruitful as well.
I was also funded through the 1990s, and performed studies on adaptation and direction selectivity,
and on development of timing in kittens. Jordan Feidler, a graduate student who had been doing neural modeling,
became the major participant in the research, along with Adi Murthy.
Jordan left before finishing his PhD because he needed to support his family,
but has served the US well at Mitre, Raytheon, and The Aerospace Corporation.
Adi continues to do research involving eye movements.
Along with Paul Baker, our programmer, we had great times in and out of the lab in Pittsburgh.
Peter Carras joined Al and me to work on replicating and extending some of our findings in monkeys.
Unlike Max Cynader, Al Humphrey and I had different strengths and weaknesses.
That of course can make for excellent collaborations,
and we put together a set of experiments that revealed exciting novel concepts and results about visual processing.
Al writes really well and understands what reviewers need, and made it possible for me to be funded.
I wish I had incorporated more of his strengths than I did.
After dozens of unsuccessful job interviews,
including for positions outside neuroscience research after I'd given up on that, I heard from Max Snodderly.
I knew Max from discussions about cortical processing. His wife, Kristen Harris,
interviewed for the department chair position in Pittsburgh but accepted a job at the Medical College of Georgia.
Max was given a position in the Ophthalmology Department. I interviewed with Max in Boston in November 2002,
walking through snowy Boston with my broken leg in an external fixator,
and he hired me to start in March 2003. Then I heard nothing from him.
I forced the issue by showing up in May, and accompanying him to a meeting with the Ophthalmology Chair,
Julian Nussbaum. Julian had me go through the processing to start in June.
Unfortunately, the university did to me what I found out they did to many people,
and didn't pay me for my first month, which led to a grave financial crisis for me that lasted many years.
Julian was my savior during most of my 18 years in Augusta, but he was fired at the end,
adding another straw that led to my retirement at the end of 2021.
I was fortunate to have Jay Hegdé come to the university.
He was a constant source of friendship, knowledge and critical thinking.
Unfortunately, the university screwed him horribly.
The administrators (including the head lawyer) who committed these crimes earned my hatred.
The final straws that made me want to retire were interference in the way I ran the graduate neuroscience course,
and the new vet and Animal Care Committee chair telling me I couldn't have music in my lab.
I'd always had music in my labs, and most of the scientists I'd admired had the same.
I was happy to retire for many reasons, but getting away from those people was important.
One of the other reasons is that I wanted to write this book.
I started it years ago, but it's impossible to do all the work that's needed for a book
while still working 60-80 hours a week. My retirement plans were altered by getting married to my wonderful wife Sarah.
Retirement has been busy, but I'm finding time for this work. I hope readers will appreciate some of the ideas herein.
At a point where this book was well along, my friend Tim Meier turned me on to his former mentor Robert Sapolsky (Tim joined his lab because there was a piano there!),
who had recently written a book about how free will is a delusion (my term).
This book has been a great inspiration in many ways, for its content as well as for its style.
I have been helped by so many people that I dare not try to mention all of them.
But like the Sapolsky book, I got a lot out of Andy Zangwill's recent biography of physicist Phillip Anderson.
Numerous other people are cited in the text. I want to clarify an important point that might be missed by most readers.
Biologists are trained to be critical. We read scientific papers to find out what's wrong with them,
not so much to learn about their content. In this book, I therefore criticize many colleagues.
These criticisms are by no means personal. They reflect different ways of thinking,
and that is kind of the point of this book, to distinguish my thinking from that of others.
I'm doubtless wrong about many things, especially because I've gone way beyond the evidence to speculate wildly.
That seems appropriate in this book that is meant for generalists as well as specialists.
The goal is to make people think, and when you find out places where I'm wrong, that's great.
I'm glad to hear from people, and will alter this book as I learn where it can be improved.
I've attempted to not write a scholarly book, in the sense that statements are always supported in the text.
Many more citations would have been nice to have for many of us, but detract from readability for most readers.
This is a choice that was difficult.
I originally organized a split stream that included far more details
that the reader could ignore by sticking to the streamlined version.
That was unwieldy, unfortunately. Perhaps a later edition will reinstate that,
but I suspect that a general audience book might be welcomed even for the scholars among us.
However, tell me where something important is missing, and I'll put it in here.
An appendix is included to provide some basics that might be useful to some readers.
It provides some information about how the experimental results are analyzed and interpreted.
A brief tutorial about neurons is followed by some relevant math ideas.
There is no single time: there is a different duration for every trajectory;
and time passes at different rhythms according to place and according to speed.
It is not directional: the difference between past and future does not exist in the elementary equations of the world;
its orientation is merely a contingent aspect that appears when we look at things and neglect the details.
In this blurred view, the past of the universe was in a curiously "particular" state.
The notion of the "present" does not work: in the vast universe there is nothing that we can reasonably call "present."
The substratum that determines the duration of time is not an independent entity, different from the others that make up the world;
it is an aspect of a dynamic field. It jumps, fluctuates, materializes only by interacting, and is not to be found beneath a minimum scale....
So, after all this, what is left of time?
You got to deep-six your wristwatch, you got to try and understand,
The time it seems to capture is just the movement of its hands... [Bob Weir lyrics to "Walk in the Sunshine"]
Let's enter the world without time.
Many of Rovelli's themes will be discussed here, especially there not being a single time, and there not being a present.
However, direction is a big focus, and in general our treatment of time is dominated by neuroscience rather than physics.
Hierarchies
It is misleading to cast brain function hierarchically, and to think that response latencies reflect such a structure.
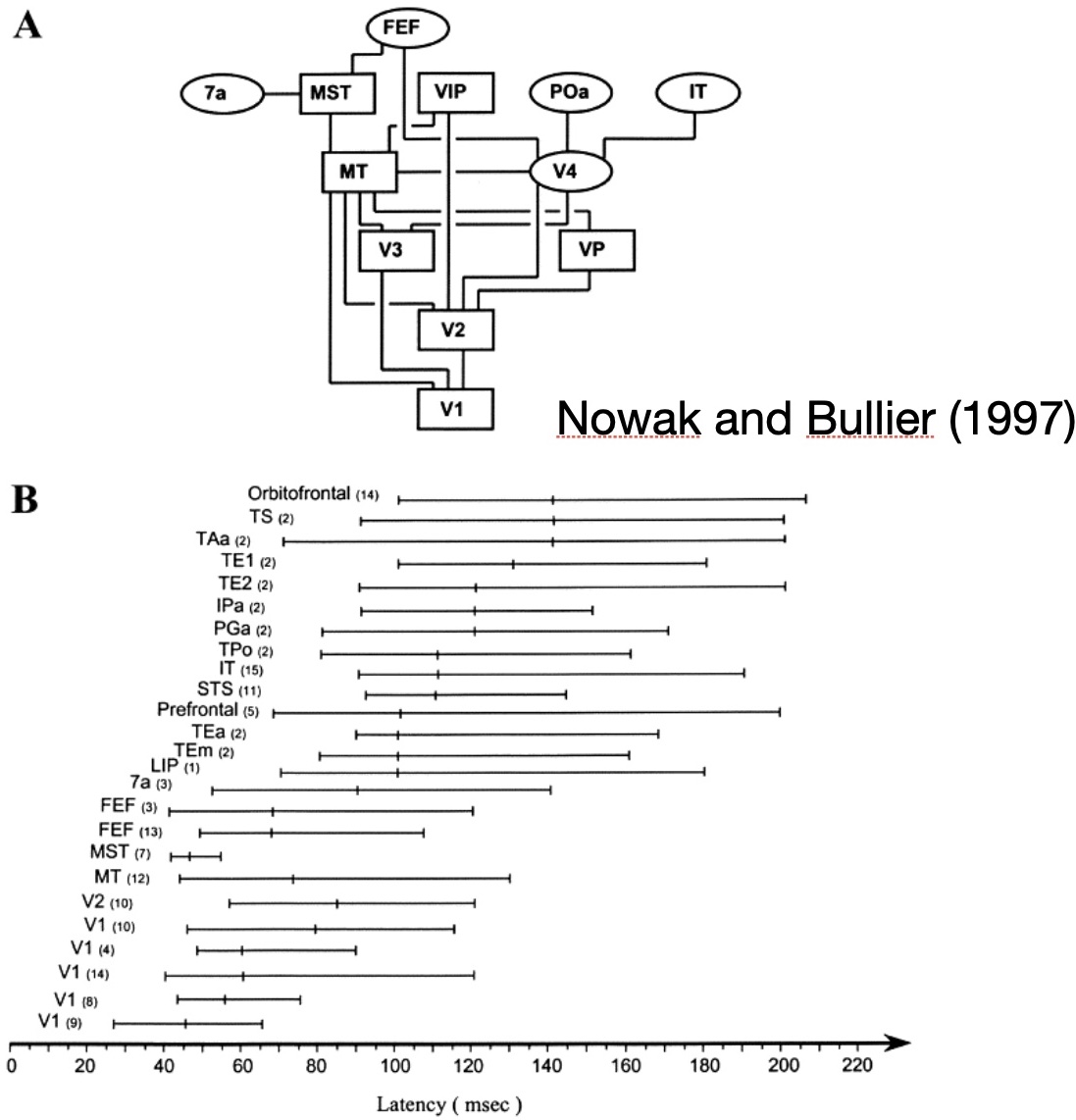
Dimensionality of time
Time is two dimensional. The dimensions are temporal frequency and phase.

Phase

Figure 4: An image of a Native American accompanies the text quoted above. I find this popular meme to be ridiculous and insulting.Latency
Latency is the slope of temporal phase vs. frequency.
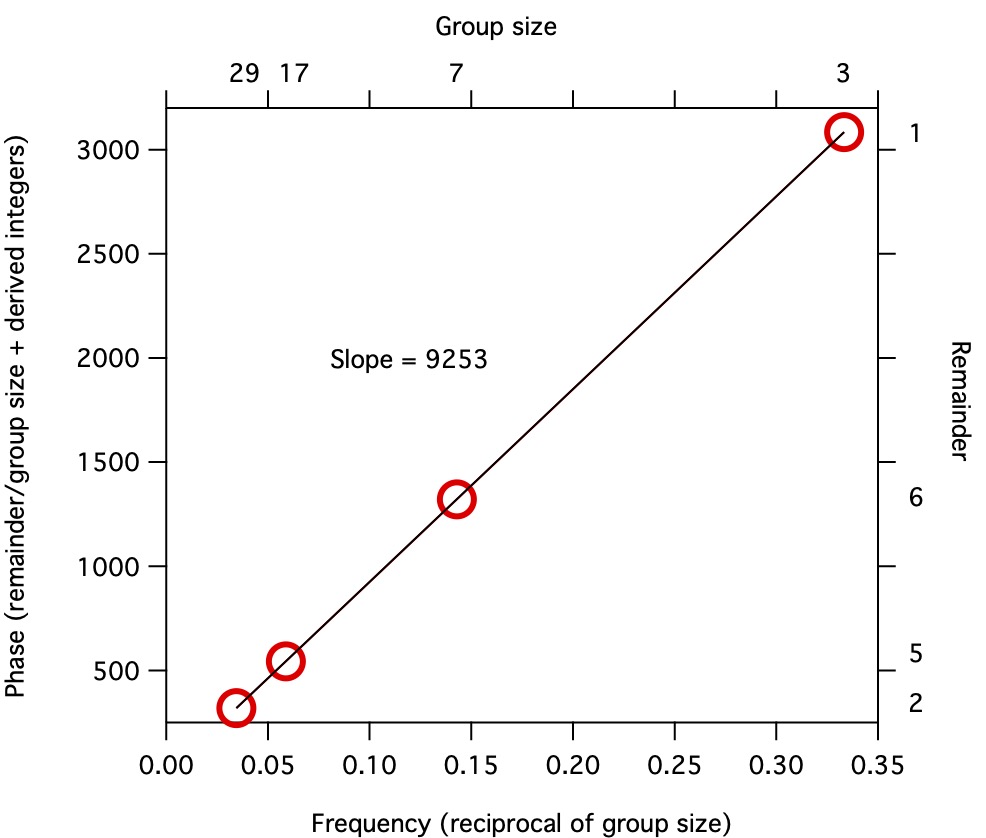
which says that the Fourier transform of a function f where time is shifted by some latency L
is the Fourier transform of f (the function F) with phase shifted by L times the frequency ω.
Even if you don't understand Fourier transforms, the point again is that the slope of phase vs. frequency is exactly latency,
the pure temporal shift of any function.10Absolute phase
The parameter with the most descriptive power when characterizing a system is absolute phase.
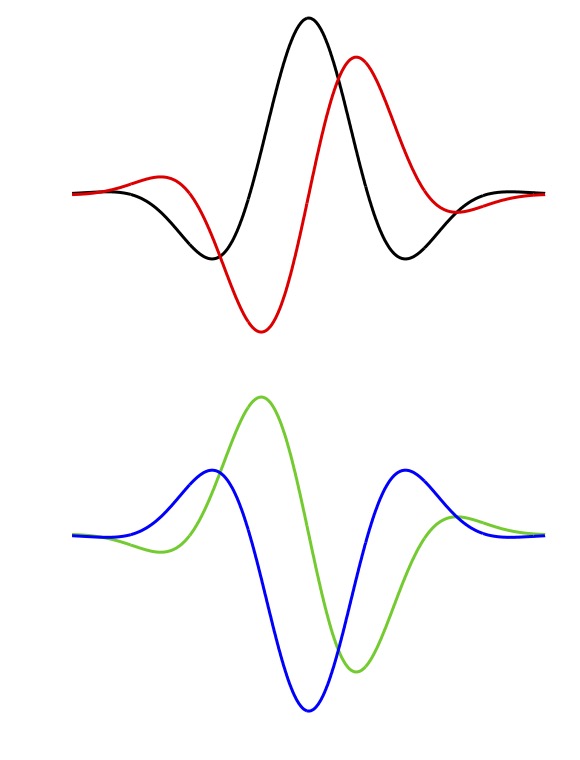
r(t)=k(t)⊗s(t) in the time domain, convolution (convoluted);
R(ω)=K(ω)S(ω) in the frequency domain, multiplication (much simpler!).Phase in the real world, especially the brain
Neurons are active during particular phases of the processes that modulate their activity.
Different neurons have different phases. This is the basis of timing, which in turn is the basis of all of our behaviors.
Transient, sustained, and lagged timing.
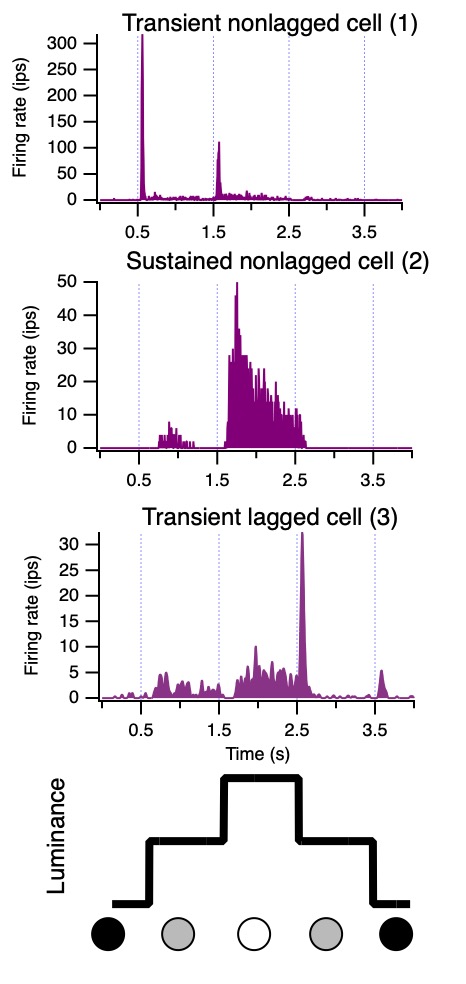
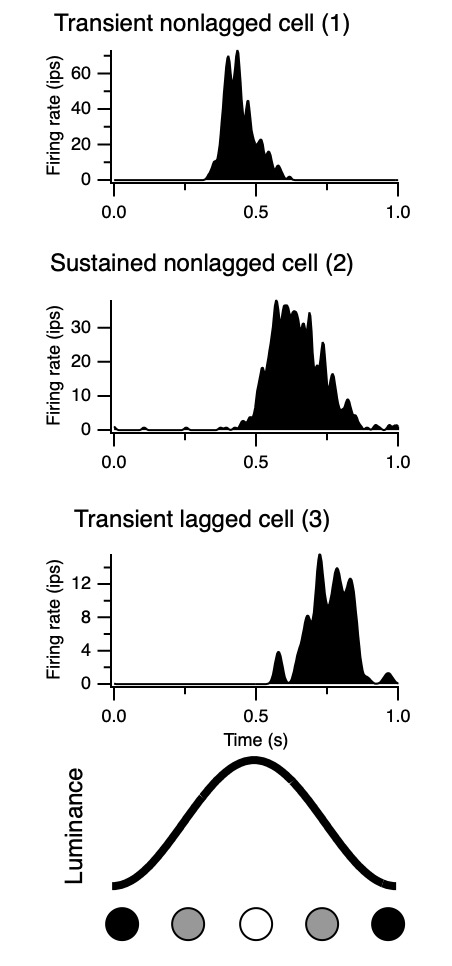
Figure 8: Sinusoidal stimulation. Responses of the cells from Figure 7 are shown for a stimulus that is modulated smoothly (sinusoidally) in time between dark and bright phases (Movie 3).
The 3 neurons fire at different phases of the stimulus cycle. The transient nonlagged cell responds slightly before the stimulus luminance peak.
The sustained nonlagged cell responds near the peak luminance, and the transient lagged cell is active well after the luminance peak.
Movie 3: Sinusoidal modulation. The spot changes between bright and dark smoothly in time. The responses of this cell are sustained nonlagged ON.
More cycles than this are typically presented, and the temporal frequency is changed from one trial to the next.
In this example the temporal frequency is 1 Hz.
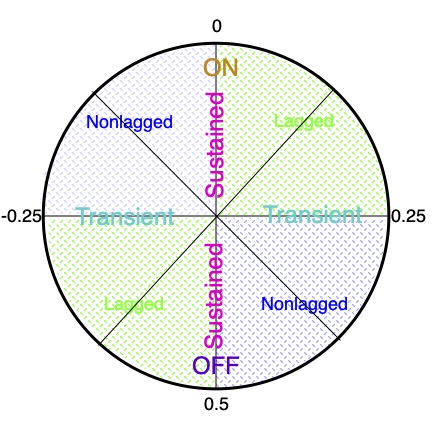
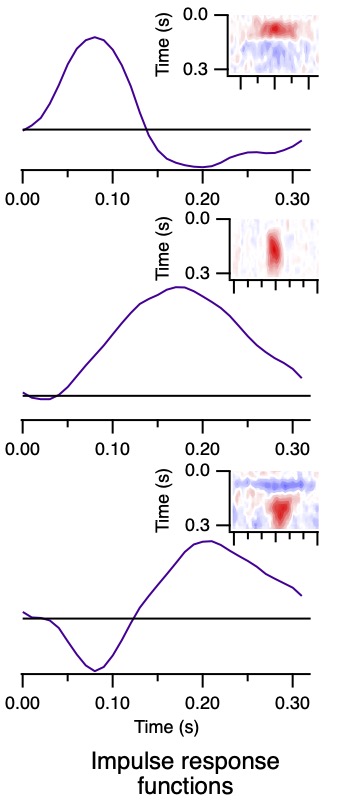
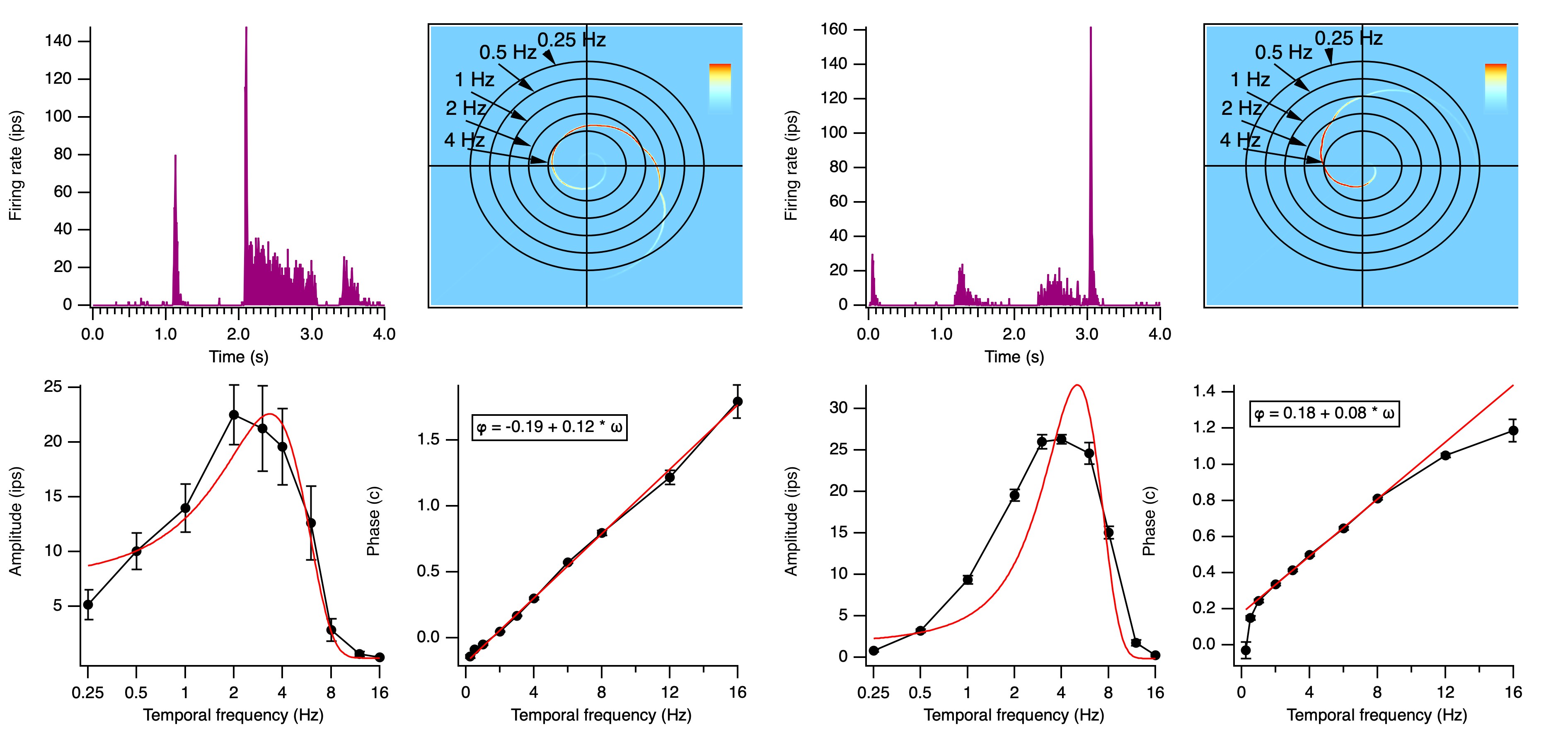
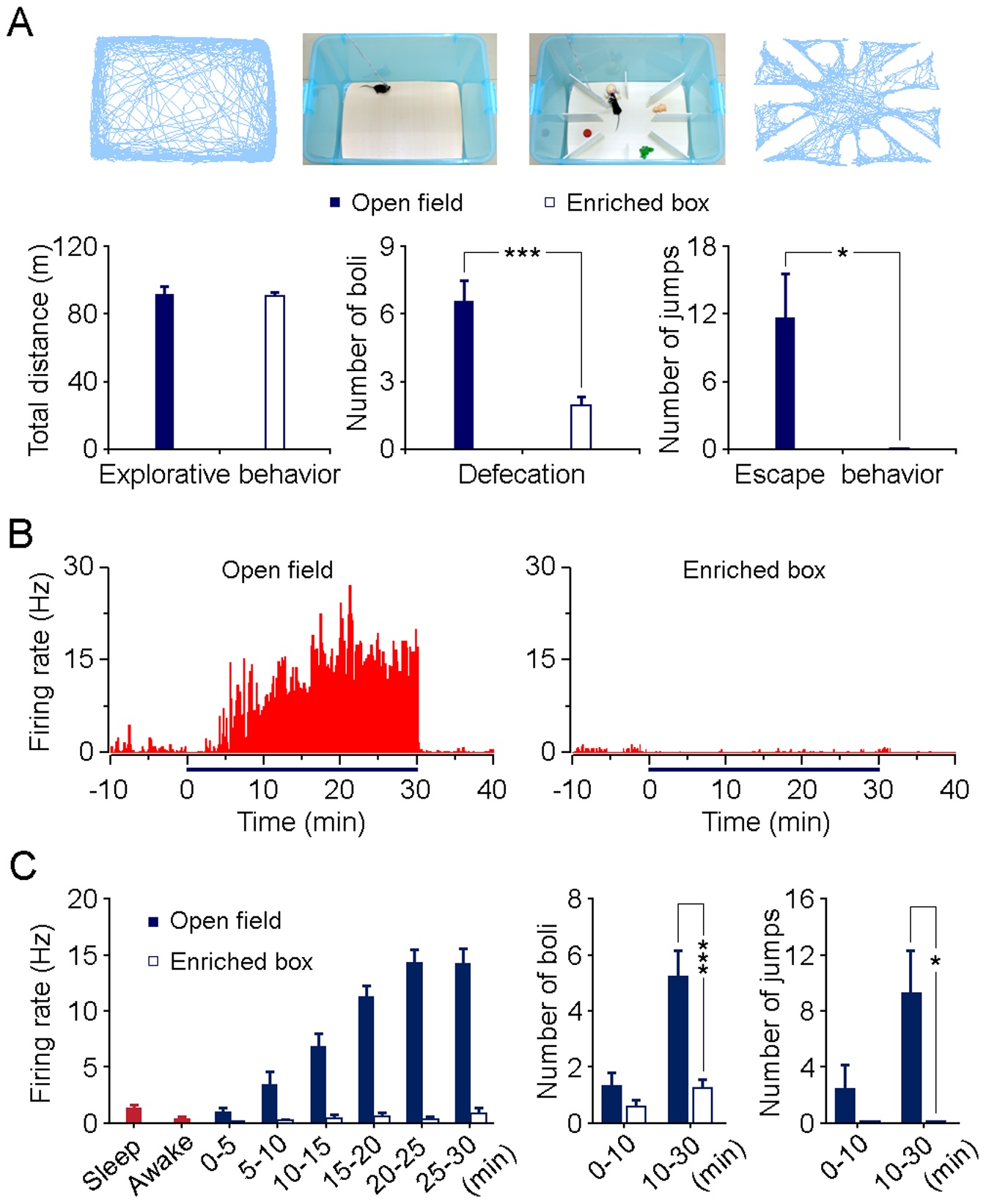
Topology of time
Continuous functions of time and their representations in two dimensions. How one- and two-dimensional time are related.

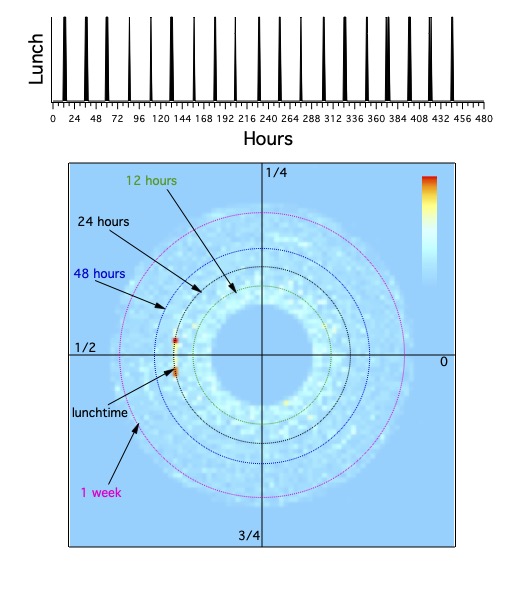

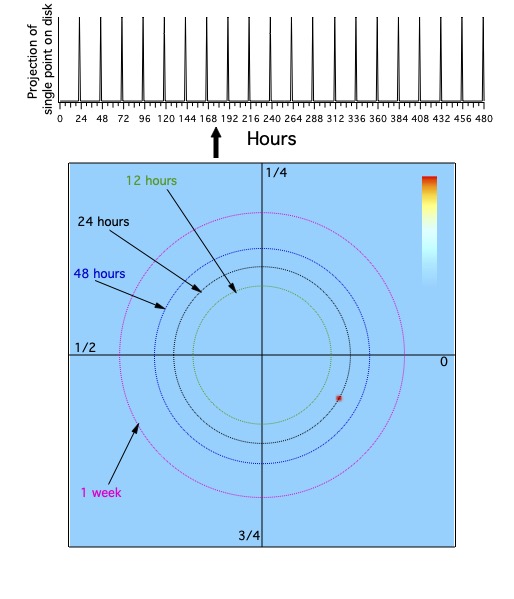
Figure 15: Disk point to line. A single point on the disk represents a period (24 hours in this case) and phase (11/12).
This point therefore projects to a series of points on the line separated by the period (24 hours here),
and occurring at the phase (about 22 hours through the day).
Figure 16: Composition of maps. A series of events that occur at a period of about 24 hours (top) is first mapped to the disk (middle),
as in fig. 11. The disk is then mapped back to the line (bottom). The resulting timeline does not match the original line at the top,
because the line and the disk differ topologically.
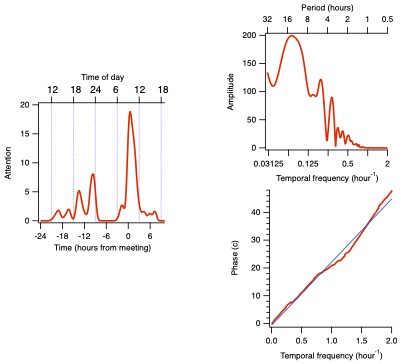
Figure 17: Time in the frequency domain. On the left is an imaginary plot of how much attention is paid to a meeting before and just after it occurs.
This time domain function is transformed to the frequency domain on the right, with components of amplitude and phase vs. frequency.
The phase vs. frequency plot at the bottom shows how phase varies fairly linearly with frequency, with a slope that is latency.
Note that amplitude is plotted against log frequency, whereas phase is plotted against linear frequency.
The deviations from linearity occur at high frequencies, above about 1/hour, where amplitudes are vanishingly small.An example of looking at both the time domain and frequency domain
How the brain lets us see across eye movements
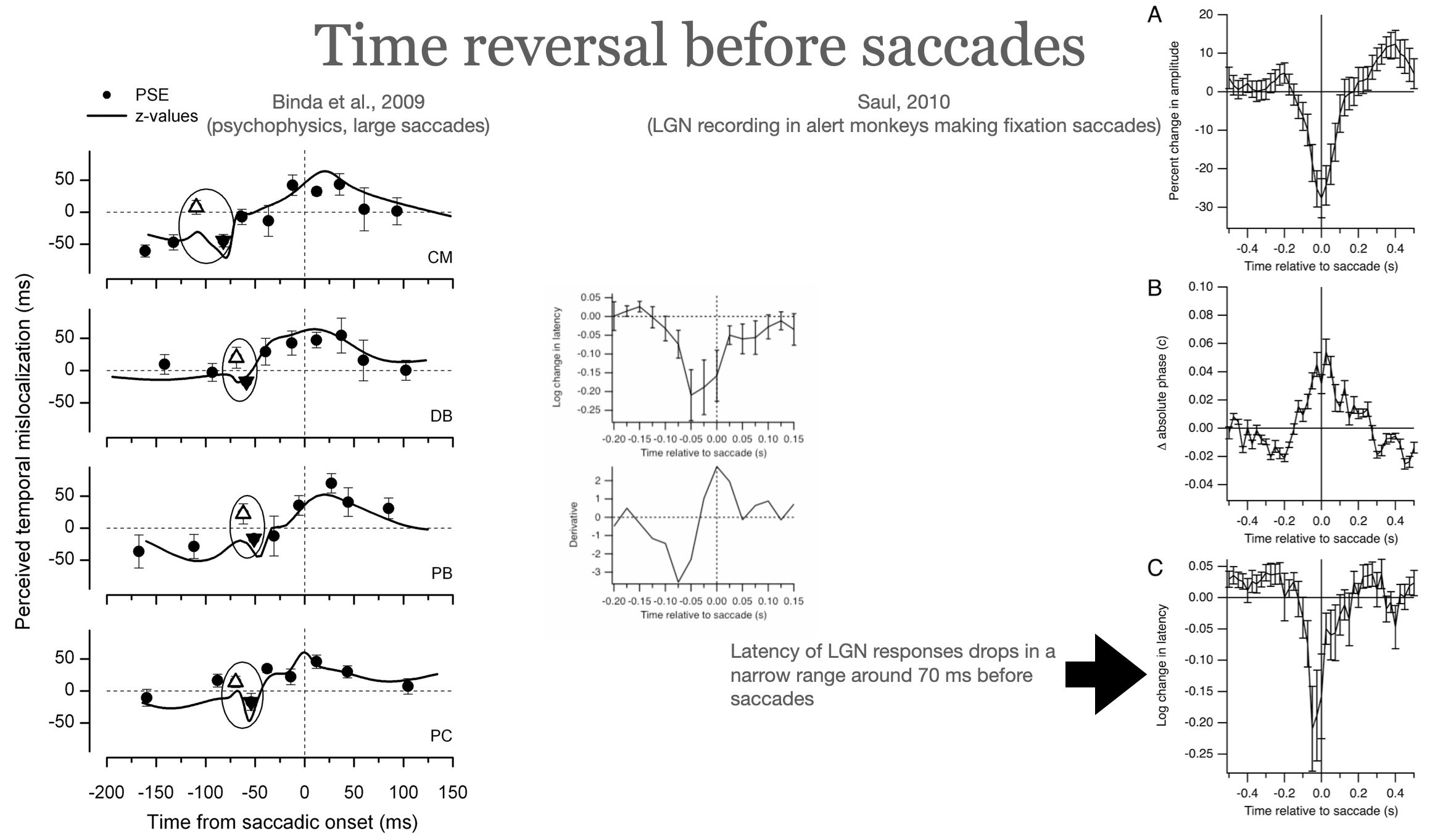
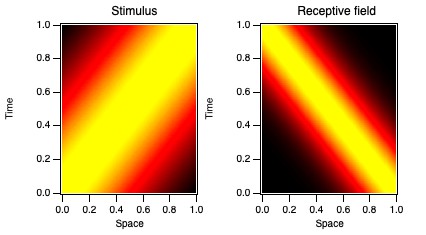
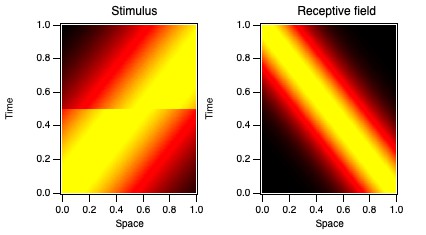
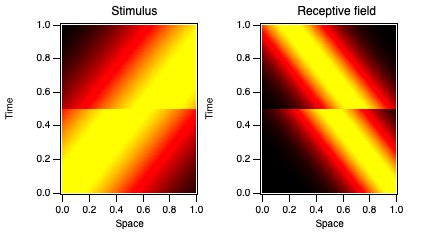
Video of clock reaction
Stitching time
Local-to-global transformations

Figure 20: Impossible welding. This photo of an object looks realistic, a triangle made from three square tubes welded together.
But it clearly does not correspond to what it looks like. The tubes could not connect with each other at the angles seen here.
The vertices where the tubes come together indicate twists that don't make sense when accounting for the whole object.
Such demonstrations are due to how our brains put together local elements into a global percept.
It also depends to some extent on presenting a spatially 3-dimensional object on a 2-dimensional surface.
Inspecting the object in three dimensions with movements would permit the illusion to disappear.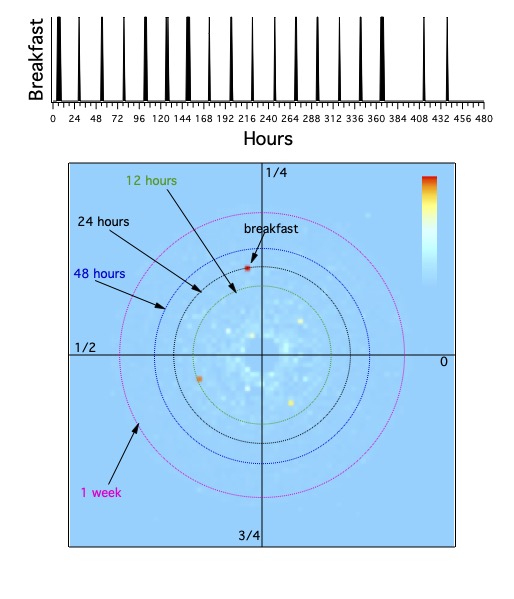

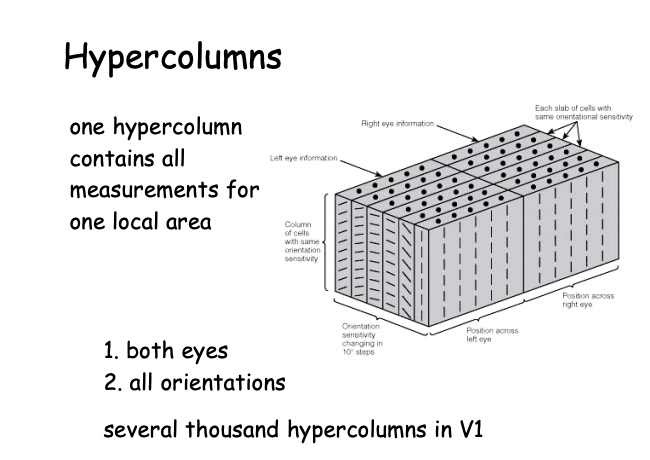
Movie 5: Sheaf in 3D. The map in Fig 23 is given a 3-dimensional representation to make clear its structure as a sheaf.
Stalks that contain the full range of colors shown in A are positioned across space,
and the stalks are cut off at the point where the appropriate color occurs.
Rotating the sheaf eventually brings it to a viewpoint that matches the scene in Fig. 23.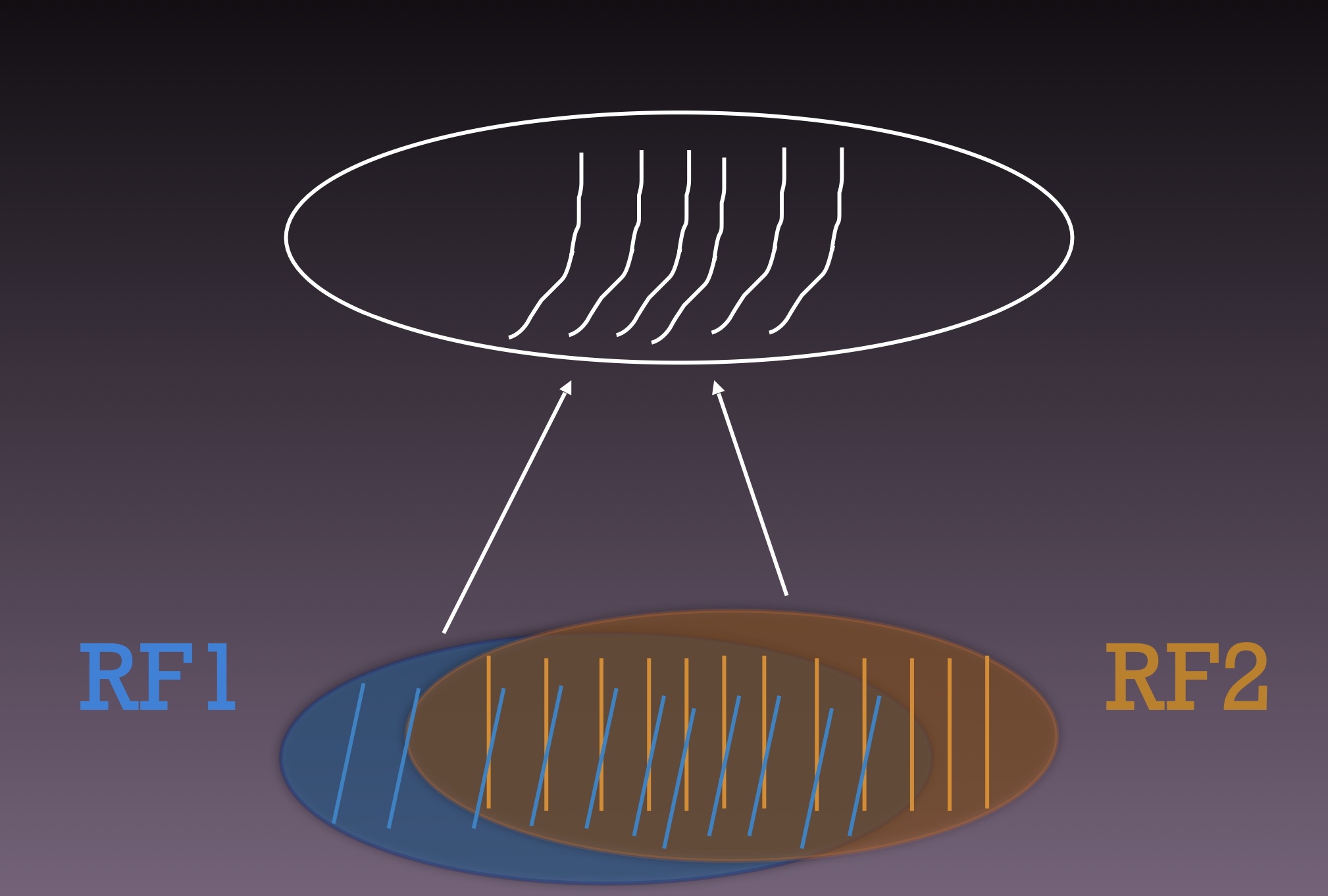
The binding problem
Putting things together, synchronously and asychronously
Emergent properties
Inputs that differ by a quarter cycle and direction selectivity
Direction selectivity
How to get direction selectivity
Spatiotemporal quadrature
The recipe
ψ - 𝜑 = 0 c
ψ + 𝜑 = ½ c
These two equations are easily solved for ψ and 𝜑. They are both true when ψ=¼ c and 𝜑=¼ c.
That is the spatiotemporal quadrature model, spatial and temporal phase differences of a quarter cycle.
Given those phase differences, you get direction selectivity.
Direction selectivity outside of visual cortex
Mechanisms that create direction selectivity in visual cortex
Lagged and nonlagged cells, latency and absolute phase, temporal frequency dependence

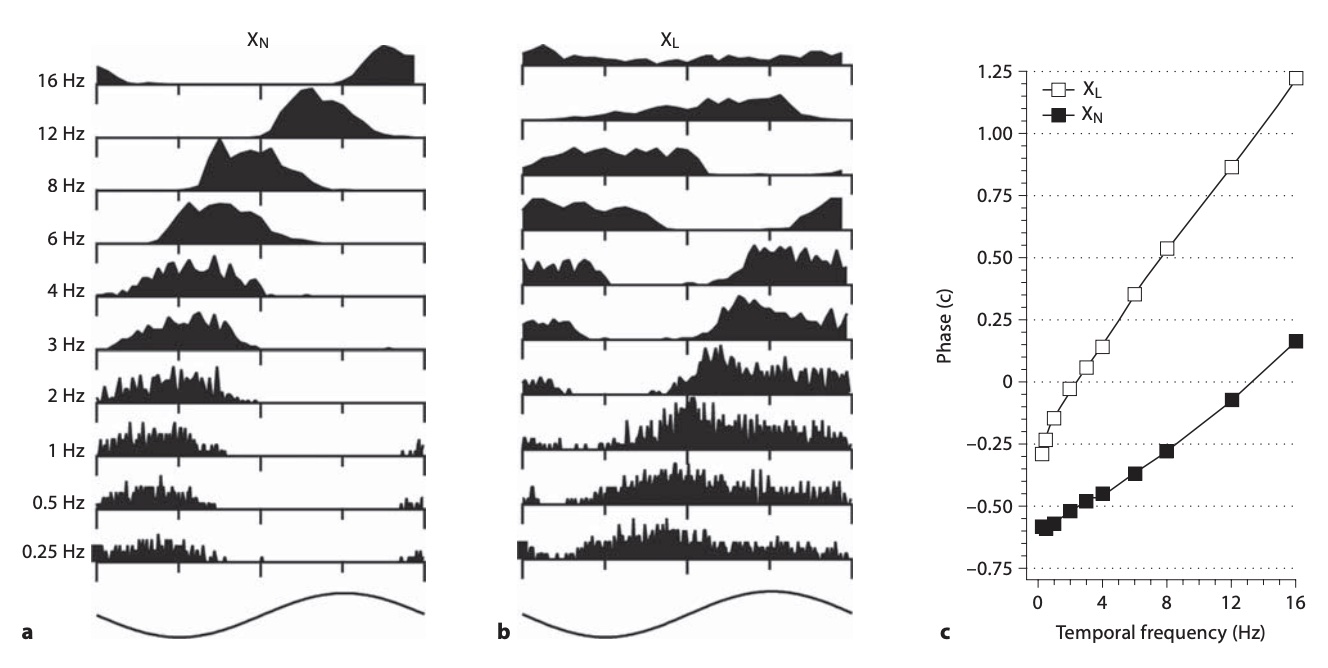
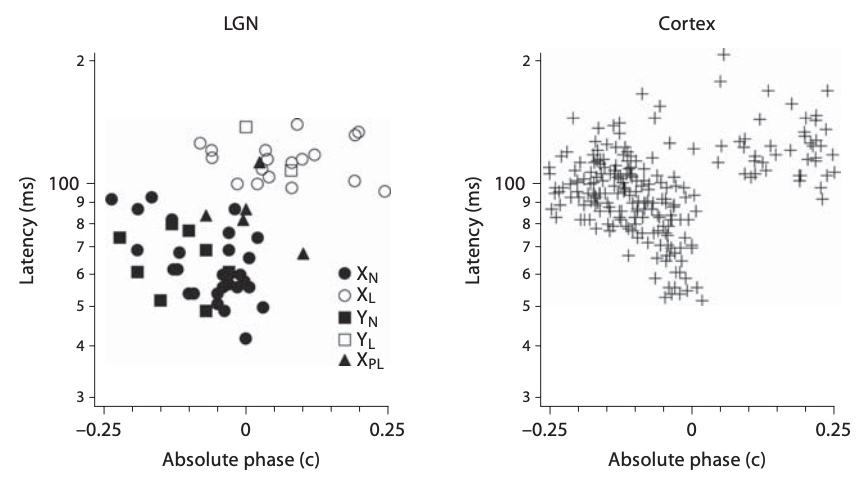
Temporal frequency tuning of direction selectivity
Loss of quadrature at high temporal frequencies in cats, but not kittens or monkeys
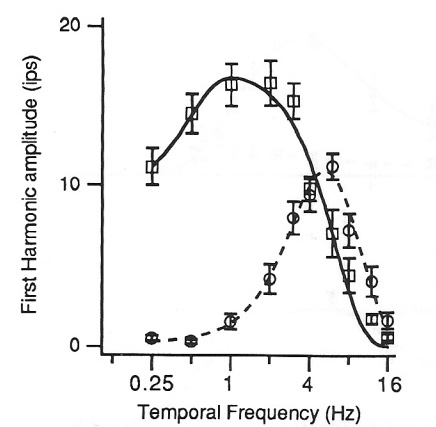
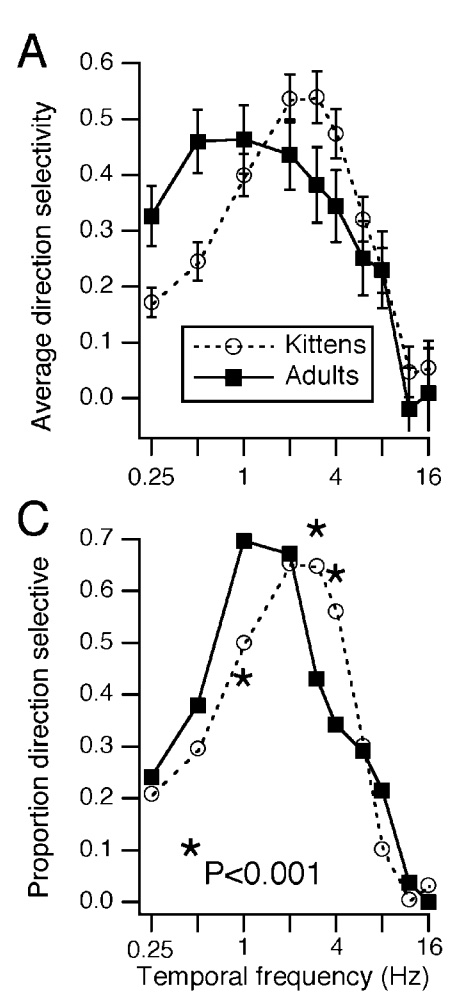
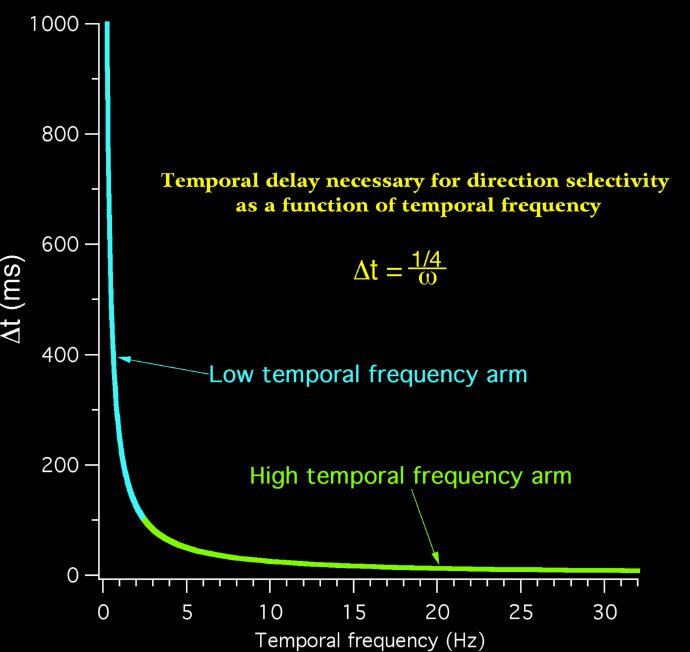
More evidence
A fun aside
Grating, dot, random, plaid, and non-visual stimuli
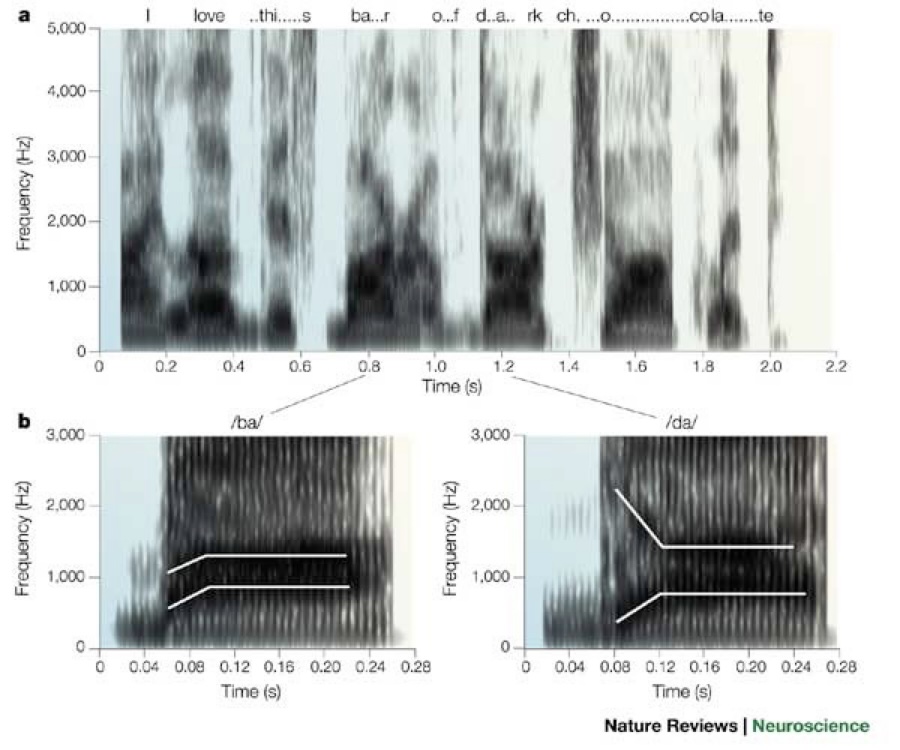
Adaptation and direction selectivity
McCollough effect
One of the most ubiquitous phenomena in sensory systems is adaptation. Adaptation can be broadly defined as changes in function due to previous experience. Importantly, "previous experience" implies that adaptation depends on time.
Typically, adapting consists of presenting stimulation that lasts a relatively long time, and the aftereffect of adapting consists of decreased function.
That can be expressed as poor responses to low temporal frequencies.
Timing aftereffect
Adaptation takes many forms, but of most interest to us is its stimulus specificity. Adapting to a grating of a particular spatial frequency makes it harder to see gratings of similar spatial frequencies, but not spatial frequencies that are much lower or higher.
This is taken as evidence that our brains have neurons tuned for spatial frequency. The idea is that adapting wears out or fatigues the neurons that are active during the adapting period, so that they no longer fire well to their preferred stimulus.
But neurons tuned to spatial frequencies that were not present during adapting were not activated and fatigued, so they remain responsive to the spatial frequencies they prefer.
That explanation doesn't hold water, since the specificity of adaptation argues against fatigue.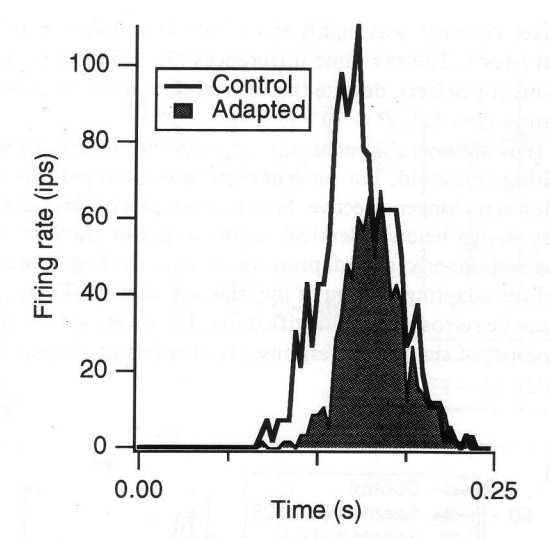
Models
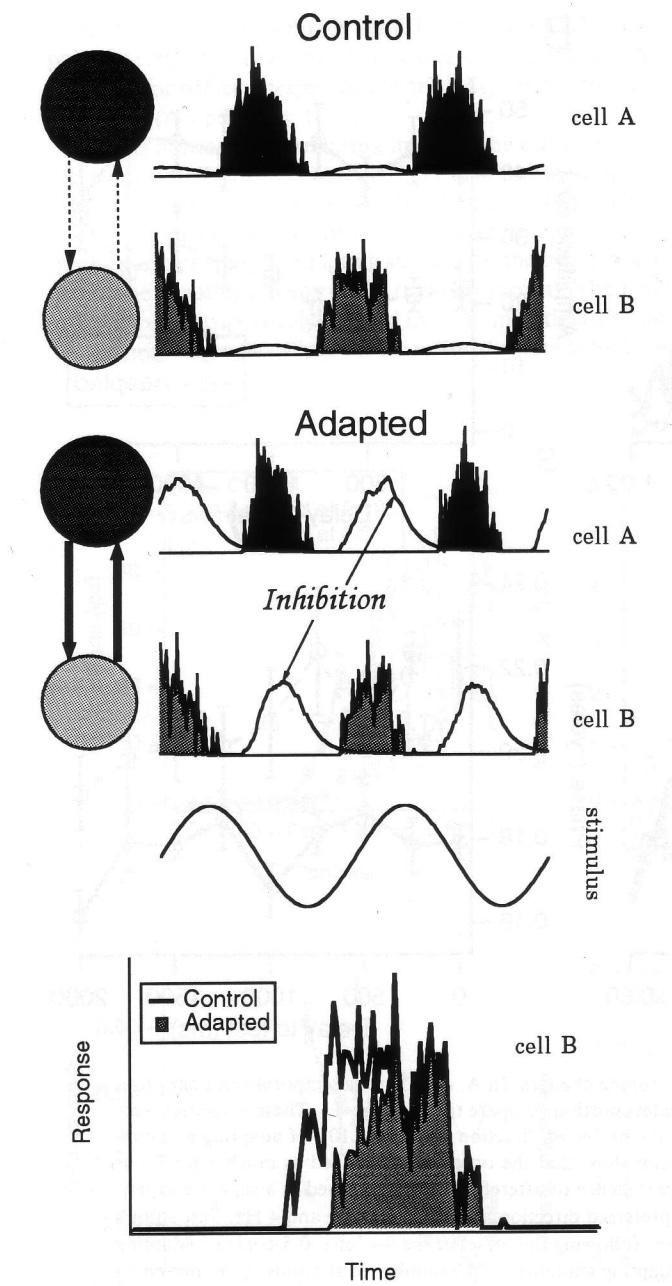
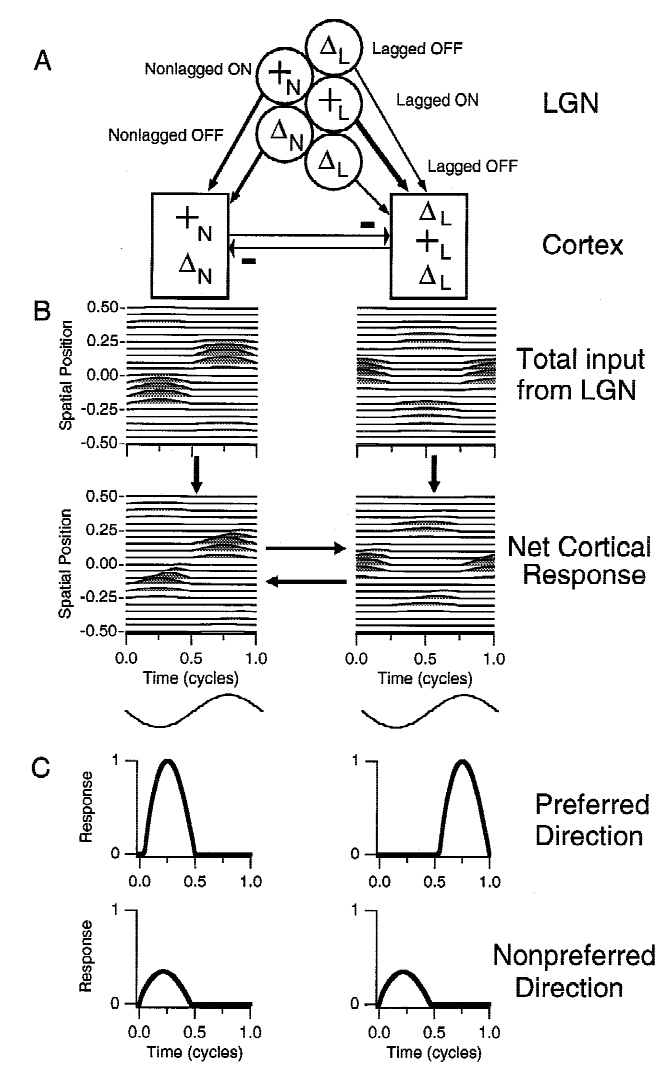
Learning direction
STDP
Postsynaptic resonance
Experience dependent modification
Motion blindness
"People, dogs, and cars appear restless, are suddenly here and then there, but disappear in between. Very often I don't even know where they have left, because they move too fast, so I lose them quite often."
Fluids appeared frozen, like a glacier, which caused great difficulty, for example, with pouring tea or coffee into a cup; filling a glass with water became impossible.
Most events were much too fast for her and she needed a considerable time to perform even simple routine activities, such as cutting bread or using the vacuum cleaner.
She could no longer use the tube, bus or tram, which severely restricted her mobility.
She also found it very irritating to meet friends and have a chat with them because she could not respond in time to their handshake and because she found their moving hand disturbing.
In addition, the experience of talking to them was very unpleasant because she had to avoid watching their (changing) facial expressions while speaking, in particular, their lips seem to "jump rapidly up and down, and I am very often unable to listen to what they were saying."
In contrast, when people, faces, objects and cars were stationary, she had no difficulty in seeing them "clearly" and could recognize them immediately and accurately.
The perception of colors had not changed, and she reported no difficulty with perceiving the position of objects and judging correctly both how far away they were and the distances between them.
She reported that reading took more time than before, writing had become somehow difficult. Psychiatric examination revealed no psychopathological symptoms, in particular depression, anxiety or agoraphobia.
LM appeared to have lost the ability to detect direction. The damage from the hemorrhage appeared to have lesioned her parietal cortex in the area homologous to area MT in monkeys.
This kind of specific injury is highly unusual, especially because it presumably needs to knock out the direction-selective cells on both sides of the brain.
18 We experience this phenomenon in discos. Movements appear jumpy.↩
Receptive fields as sheaves
Building receptive fields

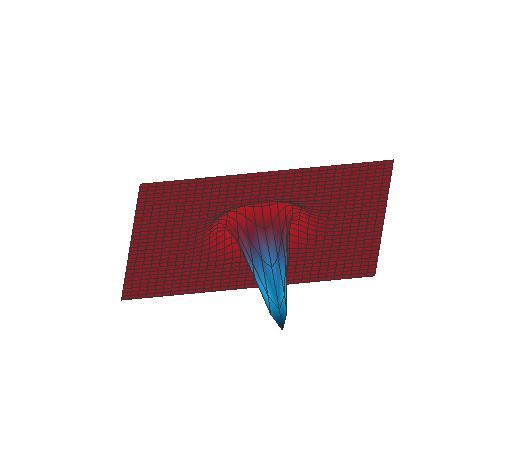

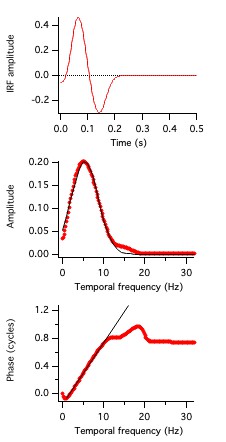
V1 RF(r,t) = Gabor1(r)*IRF1(t) + Gabor2(r)*IRF2(t).
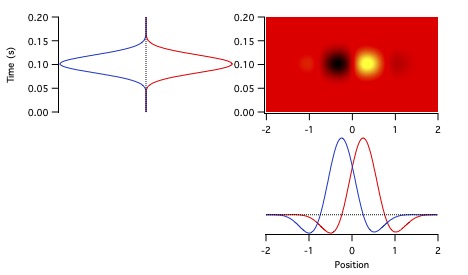
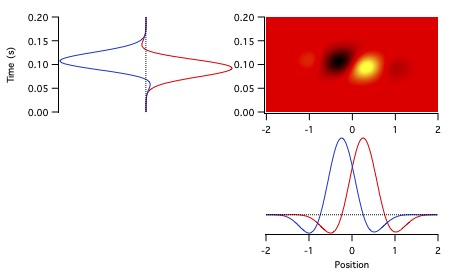
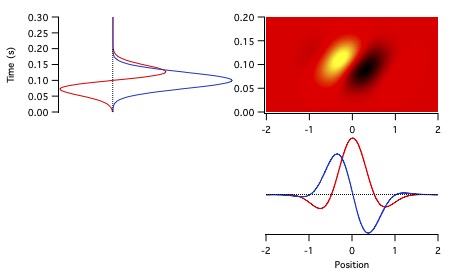
V1 RF(f,ω) = Gaussian1(f)e2πi(D1f+ψ10)∗A1(ω)e2πi(L1ω+φ10) + Gaussian2(f)e2πi(D2f+ψ20)∗A2(ω)e2πi(L2ω+φ20)
where each input has factors of gaussian amplitude and linear phase as functions of spatial frequency (f), and factors of amplitude and linear phase as functions of temporal frequency (ω).
For a classic Hubel & Wiesel simple cell, the Gaussians would be shifted in location, that is, the slope of spatial phase vs frequency (D1-D2), and the temporal absolute phases shifted (φ10-φ20) by a half-cycle (or the Gaussians would have opposite polarity).
For a direction selective simple cell, the spatial and temporal phases would each be shifted by about a quarter cycle (Figure 45).
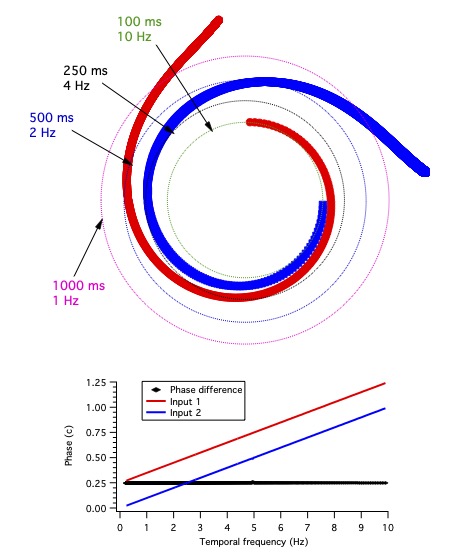
where the retinal ganglion cells project to lagged and nonlagged cells in LGN, which project to V1 to help create direction selective simple cells,
and then direction selective complex cells (which also receive inputs directly from LGN),
and those V1 cells project to MT to make direction selective neurons with large receptive fields and plaid responses.
Each of the arrows represents a projection between populations of neurons, and mathematically a set of morphisms between sheaves.
Each transformation leads to novel response properties, while ignoring properties that were present beforehand.
Globalization
Direction selectivity and loss of retinotopy
Accessory optic system
MT
LIP
Behavior
Sustained/transient/lagged
Thalamus
Cerebellum
Physics and Philosophy
One-dimensional time
The direction of time
Causality
Dependence on phase
Biases in direction selective populations
Music
Stephen Foster melody in 12 keys (C, G, D, A, E, B, F♯, D♭, A♭, E♭, B♭, F)
"Dear Friends: I have the joy of being able to tell you that, though deaf and blind, I spent a glorious hour last night listening over the radio to Beethoven's "Ninth Symphony."
I do not mean to say that I "heard" the music in the sense that other people heard it; and I do not know whether I can make you understand how it was possible for me to derive pleasure from the symphony.
It was a great surprise to myself.
I had been reading in my magazine for the blind of the happiness that the radio was bringing to the sightless everywhere. I was delighted to know that the blind had gained a new source of enjoyment; but I did not dream that I could have any part in their joy.
Keller describes how music depends on time better than any hearing person I've encountered.
Film
Movie 22: Michael Snow's Wavelength. Probably the best known example of slow cinema.
Movie 23: Andy Warhol's Empire. A clip of a much much longer film.
Movie 25: Clip from Frank Borzage's "Little Man, What Now?".
Movie 26: Excerpt from an interview of Masahiro Shinoda, mainly discussing Mizoguchi's film "Ugetsu".
Arguing
Appendix
Basics of neurons
Sapolsky includes an excellent, and much longer appendix about basic neuroscience. Here is a terse version.
Visual neurophysiology
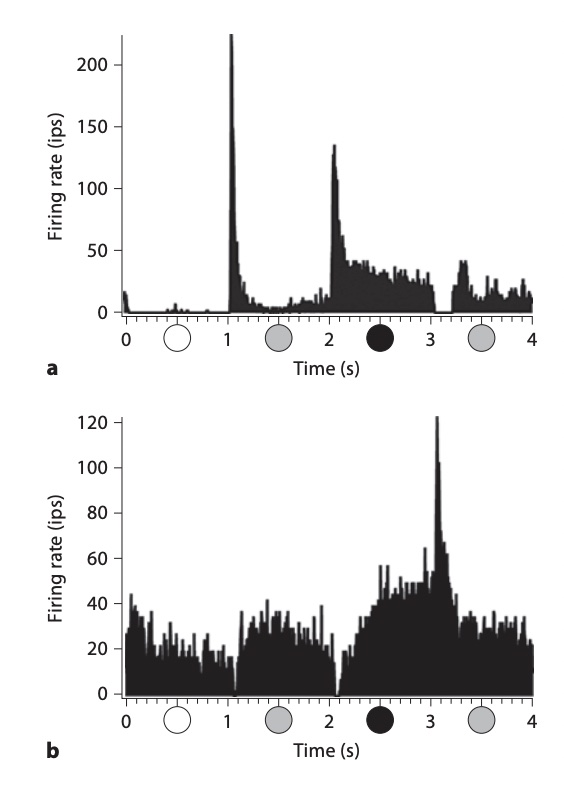
Afterword
Some biographic information. My path through time
The Clock Reaction
Video of clock reaction
Dedicated to two non-scientists who nonetheless were major influences on this work: Art Manion and the late Jackie Hughes.
Thanks to many many people. The great folks at WaveMetrics, makers of Igor Pro, deserve enormous recognition.
Special thanks to A.G. for his help with the 3-D sheaf viewing.